Computing Maximum-Area Sections of Convex Polyhedra
Extensions
Next, we'll describe an application and some further work on the problem we've been considering.
Application in shape-matching
Although the problem is interesting in its own right, the algorithms for solving it that we've looked at can also be used to solve another, rather different problem, one with applications in shape-matching and shape-recognition:
Let P and Q be convex polygons. Given a direction in which to translate P, find the translation which maximises the overlap between P and Q.
We are given two convex polygons, P and Q, in the xy plane and some vector v along which P is to be translated. Let's add a third dimension to this scenario and consider the xy plane to be a plane in xyz space. We let Q become a cylinder protruding orthogonally out of the xy plane. Formally, Q points in the direction (0, 0, 1). On the other hand, we let P become a slanted cylinder, pointing in the direction (vx, vy, 1), where vx and vy are the x and y components of our translation vector v. The intersection of these two cylinders forms a polyhedron K (which might, of course, be empty).
Visually, translating P by vector v corresponds to moving along the z-axis. On the plane z = 1, we've effectively translated P by v. On the plane z = 2, we've translated P by 2v, and so on. For every value of z, say a, the area of the intersection between K and the plane z = a gives the area of overlap between P and Q when P is translated by the vector av.
All we must do is find the plane z = a, perpendicular to the z-axis, that induces the maximum area section through K. Then, the maximum-overlap translation of P in the direction v will be of magnitude a. If we can compute the intersection of our cylinders P and Q in linear time, then, assuming that K is convex, we can use our algorithms from the previous page to do this in linear time. It's easy to convince oneself that the intersection of two convex polyhedra is also convex (a straightforward proof by contradiction works). Then, since both P and Q are convex, their intersection must be convex, too.
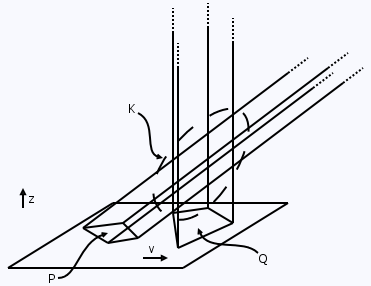
Q becomes a cylinder orthogonal to the xy plane, P becomes a slanted cylinder, pointing in the direction (vx, vy, 1). We run our algorithms on the intersection (in the dashed region), sweeping our plane perpendicular to the z-axis.
Although we won't go into the details here, Chazelle describes, in [5], a linear time algorithm for finding the intersection of three-dimensional convex polyhedra. Our cylinders are certainly convex, so his algorithm works in our case. This gives a linear time algorithm for the shape-matching problem described above. Of course, our algorithms assume that our sweeping plane is perpendicular to the x-axis. However, as mentioned in the introduction, it's easy to rotate, in linear time, any convex polyhedron such that the direction we are actually interested in lies along the x-axis. More cleverly, of course, in this case, we could simply define our polygons P and Q to lie in the yz plane and let the cylinders we construct out of them point into a positive x-direction. It's just a question of interpretation, nothing really changes.
Sectional area in Rd
In addition to the algorithms we have covered, Avis et al describe, in [1], a linear time algorithm for our problem in arbitrarily many dimensions:
Let K be a convex polytope in Rd and let A(a) be the area/volume of the intersection between K and the hyperplane x = a. Find the value of a that maximises A(a).
Although we won't go into the details here, the algorithm given in [1] uses the unimodality of sectional area/volume of convex polytopes in any number of dimensions to apply a prune-and-search approach to the sectional area/volume function. Recall that in proving the unimodality of sectional area of convex polyhedra, we used the Brunn-Minkowski theorem, which holds in any number of dimensions. Thus, sectional area/volume is a unimodal function for polytopes in any number of dimensions.
Next: Applet.