Computing Maximum-Area Sections of Convex Polyhedra

Algorithms

Here, we'll present a number of algorithms to solve the maximum-area section problem for convex polyhedra. We'll proceed in order of decreasing time complexity, culminating with a linear time algorithm. Before we do so, however, let's look at the special case that our polyhedron K is a convex drum.

O(n) time algorithm for convex drums

Recall that the sectional area function of a drum is quadratic. More precisely, we saw that the sum

A(P) = (1/2) Sum_1<=i<=n (p_{i-1_y}p_{i_z} - p_{i-1_z}p_{i_y})

is a quadratic function in q, where x = qx₁ + (1-q)x₂ is the plane slicing through our drum whose vertices are on the planes x = x₁ and x = x₂. So if A(a) is the sectional area function of a drum, then A(a) itself is some quadratic function in q. Now, using elementary calculus methods, we can find the first derivative of A(a) and equate it to zero: A'(a) = 0. Solving for a will give the maximum of A(a). We know that since our drum is assumed to be convex, A(a) is a strictly unimodal function. So any point at which the derivative A'(a) is zero must be in the global maximum region. Since A(a) is a quadratic function, it is easy to compute the derivative A'(a).

What would the running time of this algorithm be? First, we must symbolically find A(a) in terms of q. Recall that the sum above expands to

A(P) = (1/2) Sum_1<=i<=n (q²(v_{i-1_y}v_{i_z} - v_{i-1_y}w_{i_z} - w_{i-1_y}v_{i_z} + w_{i-1_y}w_{i_z} - v_{i-1_z}v_{i_y} + w_{i-1_z}v_{i_y} - w_{i-1_z}w_{i_y} + v_{i-1_z}w_{i_y}) + q(v_{i-1_y}w_{i_z} + w_{i-1_y}v_{i_z} - 2w_{i-1_y}w_{i_z} - v_{i-1_z}w_{i_y} - w_{i-1_z}v_{i_y} + 2w_{i-1_z}w_{i_y}) + (w_{i-1_y}w_{i_z}-w_{i-1_z}w_{i_y})),

where (v_i, w_i) is the long edge from plane x = x₁ to plane x = x₂ that intersects x = qx₁ + (1-q)x₂ at point p_i of the polygonal section whose area we are computing. In the above expansion, we need to know how the long edges around K are ordered, to know how the p_i's are ordered. We could sort them, but this is unnecessary. The easiest way to do this is to traverse the faces of the drum in order, avoiding the "end-polygons" lying in the planes x = x₁ and x = x₂. Since we assume our drum is represented by a winged-edge data structure, this takes constant time per edge, or O(n) time in total. Considering the edges between these faces gives us their ordering. This must only be done once. Once we have an ordering of the long edges, we are able to evaluate the sum above in earnest to give us an actual quadratic function of q. Having A(a), computing the derivative A'(a) and solving for a in A'(a) = 0 takes constant time, since A(a) is quadratic. Thus, the running time is dominated by the traversal step, so the entire algorithm takes time O(n).

Algorithm Drum-MaxSecArea(K : convex drum)

Find x = x₁ and x = x₂.

Find any face of the drum bounded by a long edge.

Traverse the faces of the drum, avoiding the end-polygons. Maintain a list of all edges crossed this way.

Using the ordering from the list obtained above, symbolically compute A as a quadratic function of q.

Symbolically compute A' as a linear function of q.

Solve A'(a) = 0 for a.

Return a.

While we're here, let us define an algorithm based on the above that will allow us to compute the actual sectional area obtained by intersecting some plane x = a with an arbitrary drum K:

Algorithm Drum-SecArea(K : drum, a : real)

Find x = x₁ and x = x₂.

Find any face of the drum bounded by a long edge.

Traverse the faces of the drum, avoiding the end-polygons. Maintain a list of all edges crossed this way.

Using the ordering from the list obtained above, symbolically compute A as a quadratic function of q.

Find the value of q such that a = qx₁ + (1-q)x₂.

Evaluate and return A(q).

We will see that this algorithm will come in handy in several places. It's running time, like that of Drum-MaxSecArea, is O(n). Note, however, that the first four steps need only be carried out once per drum. After this, we can find cross sectional areas of that drum in essentially constant time.

You might be interested in the following, simpler approach for the second algorithm: Instead of carrying out the face traversal to obtain the long edge ordering, simply compute the points of intersection between all edges and the slicing plane (this takes constant time per edge, or O(n) time in total), then radially sort these points around one of them. This takes O(n lg n) time and the resulting ordering can be used to find the area of the section. This is slower than the algorithm described above, but is far easier to implement.

Note also that in actually computing the sectional area of a drum, we don't need any unimodality properties. So the algorithm Drum-SecArea works for arbitrary (possibly nonconvex) drums.

O(n²) time algorithm for convex polyhedra

Now, we can easily construct a simple algorithm for arbitrary convex polyhedra using Drum-MaxSecArea. Suppose we're given an arbitrary convex polyhedron K. Consider passing a plane perpendicular to the x-axis through every vertex of K. Now, by computing the points of intersection between these new planes and the edges of K, we can introduce new points that partition edges. By this partitioning, every segment between two adjacent planes forms a drum. Now, we can just apply Drum-MaxSecArea on each of these drums to obtain their respective maximum area sections. After this, we return the maximum-area section of the entire polyhedron K by using Drum-SecArea to find the actual sectional areas of the found maxima and remembering the largest one found and the drum it was found in.

Note that we could be cleverer here and use the unimodality of the sectional area function of K to not have to compute the actual sectional areas using Drum-SecArea. However, this would not change the time complexity of this particular algorithm, so we will leave this cleverness to another algorithm.

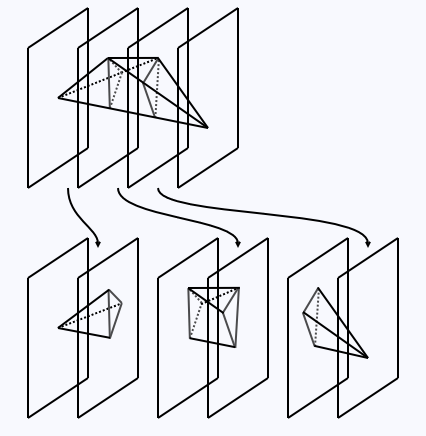
Partitioning an arbitrary convex polyhedron into drums.

What is the running time of this algorithm? Observe that constructing the points of intersection between our planes and the edges of K will yield O(n) vertices for each drum (since each plane can intersect at most O(n) edges), of which there are O(n). Thus, we are left with O(n²) vertices over O(n) drums. Applying Drum-MaxSecArea on all drums thus takes time O(n²) and computing the actual sectional areas also takes time O(n²). Choosing the maximum from these values takes time O(n). The O(n²) terms dominate, yielding a total running time of O(n²).

Algorithm Quadratic-MaxSecArea(K : convex polyhedron)

For each vertex v of K, construct a plane x = v_x.

Compute the points of intersection between the planes x = x_i and the edges of K. Let them be new vertices that partition the edges of K.

For every pair of adjacent planes x = x_i and x = x_i+1, define a drum D_i between them, made up of the vertices in x = x_i and x = x_i+1 and the edges between them.

For every drum D_i defined this way, find a_i = Drum-MaxSecArea(D) and d_i = Drum-SecArea(D, a_i). Remember the maximum d_i obtained and return the corresponding a_i.

O(n lg n) time algorithm for convex polyhedra

In Quadratic-MaxSecArea, we ran Drum-MaxSecArea and Drum-SecArea on every drum we constructed from our original polyhedron K. Note that we didn't make use of the fact that the sectional area function of K is unimodal. We only used this fact for the drums we created. An easy improvement to our algorithm above is to apply binary search on the constructed planes. That is, rather than creating all the O(n) drums again, we construct our O(n) planes and, in linear time, find the median plane x = x_m (see [4] for more information on median-finding in linear time). Now, we construct the single median drum between x_m and x_m+1 and use Drum-MaxSecArea to find the plane that provides the maximum-area section in it. If this plane is somewhere in the interior of the drum, we have found the maximum sectional area of the entire polyhedron. This follows from the strict unimodality of our polyhedron's sectional area. If the plane is one of the extremal planes of the drum (the "end-planes"), we know that the plane inducing the maximum-area section for the entire polyhedron must lie on this side of the polyhedron, too. Thus, we recurse on the median plane of the remaining portion suggested by the position of the maximum-area section plane just computed.

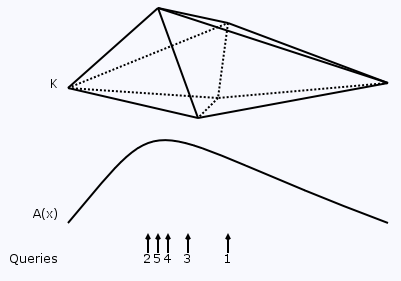
Exploiting the unimodality of A(a) in applying binary search.

This algorithm is a fairly classical application of binary search, and it is easy to see that we construct and consider O(lg n) drums in this approach, rather than the O(n) we were considering previously. Each drum has O(n) vertices, so constructing the vertices of each drum and running Drum-MaxSecArea on it requires O(n) time. Thus, this algorithm has total running time O(n lg n).

(See [4] for more information on the binary search principle and its common running times.)

Wrapper BinarySearch-MaxSecArea(K : convex polyhedron)

Find x = x₁ and x = x₂.

For each vertex v of K, construct a plane x = v_x.

Run BinarySearch-MaxSecArea(K, x = x₁, x = x₂).

Algorithm BinarySearch-MaxSecArea(K : convex polyhedron, lo : plane, hi: plane)

Let x = x_m be the median plane between lo and hi. Construct a drum D between x_m and x_m+1.

Find a = Drum-MaxSecArea(D). If a = x_m, run BinarySearch-MaxSecArea(K, lo, x = x_m). If a = x_m+1, run BinarySearch-MaxSecArea(K, x = x_m+1, hi). Otherwise, return a.

Note that in the above, we assume we can find the plane x = x_m+1, given x = x_m. Since our algorithm runs in time O(n lg n), we can, in preprocessing, sort the constructed planes by x-coordinate without affecting the running time of our algorithm (recall that sorting can be done in O(n lg n) time). This gives us an easy way to find x = x_m+1, given x = x_m.

These algorithms are all nice and good, but they're not linear time. It's time to go the whole nine yards.

O(n) time algorithm for convex polyhedra

You'll have noticed that we really haven't used all that much of the theory we built up on the background page and are justified in expecting to get your money's worth. Now, we'll use all that material to describe a linear time algorithm for the problem. We'll again use binary search, but we'll decrease the complexity of our polyhedron as we go, using the near-drum cutting operations discussed before.

Our first convex polyhedron K is a near drum with n vertices. Recall that near-drums can be decomposed into drums and a simpler near-drum in O(n) time. In particular, the near-drum we're left with has complexity O(k), where k is the total degree of the inner vertices of the initial near-drum. At every point in the algorithm, we will maintain a near-drum P (which starts off as our polyhedron K) with some area function A_P(a) for x₁ <= a <= x₂ and a collection of drums, for which we will maintain a total area function A_D(a) for x₁ <= a <= x₂. This total area function will be the sum of the sectional area functions of all the drums we have cut off our near-drum. Since each of these functions is quadratic in a, the function A_D(a) itself will be quadratic in a. Notice that if A(a) is the area function of our entire polyhedron, then A(a) = A_P(a) + A_D(a).

It's important that at every step, we force the complexity of our near-drum to be proportional to the total degree of its inner vertices. Suppose that the end-planes x = x₁ and x = x₂ each contain a single vertex. In this case, the number of vertices of the near-drum is obviously proportional to the number of inner vertices, and, since the near-drum is convex, also to the number of edges and thus also to the total degree of all inner vertices.

How do we begin? Given a convex polyhedron K, we let A_D = 0 and we find the supporting planes of K parallel to the x-axis, x = x₁ and x = x₂. In effect, this simply involves finding the vertices with lowest and highest x-coordinate, respectively. This takes time O(n). If either plane x = x₁ or x = x₂ contains more than a single vertex, we might have to cut off some drums to force the complexity of K to become proportional to the total degree of its inner vertices. We'll describe exactly what we do when cutting off drums shortly.

How do we go about updating and manipulating A_P and A_D and cutting off drums to ensure that the properties outlined above continue to hold at every step of the algorithm? First, we will, in linear time, find the vertex in P which has median x-coordinate x_m and form the median plane x = x_m. We will evaluate the derivative at this median, A'(x_m). Since A(a) = A_P(a) + A_D(a), we know that A'(a) = A'_P(a) + A'_D(a). At every step, we know A'_D, since A_D is quadratic which we will maintain, and we can obtain A'_P(x_m). To obtain A'_P(x_m), we can, for instance, proceed as follows:

We have plane x = x_m, and we construct a plane x = x_m + epsilon, where epsilon is some positive constant smaller than the x-distance between any two vertices of P (we will discuss how to find this later). Since the complexity of P is O(k), where k is the total degree of K's inner vertices, K has at most O(k) edges, so we can, in O(k) time, construct a drum between these two planes and find the quadratic area function of this drum. Then, after computing the first derivative of this function, we can evaluate it at x_m to find A'_P(x_m). This entire procedure takes time O(k).

This way, we can find b = A'(x_m) in O(k) time. Bear in mind that since the complexity of our near-drum P is assumed to be O(k), finding the median plane x = x_m can be done in O(k) time, too. Now, if b = 0, we have found the maximum sectional area. If b < 0, we will recurse on the interval [x₁, x_m]. If b > 0, we will recurse on the interval [x_m, x₂].

Suppose, without loss of generality, that we recurse on the interval [x₁, x_m]. The first thing we do is let x₂ = x_m. In other words, we shorten our near-drum P to obtain a new near-drum P' that contains at most half as many inner vertices as P. Of course, the complexity of P' is not necessarily proportional to the degree of its inner vertices. Thus, we now perform our near-drum cutting operation as many times as necessary to reduce P' to a near-drum of complexity O(k'), where k' is the total degree of the inner vertices of P'. This yields some drums, all of which have quadratic area function. Thus, they can be added to our growing drum area function A_D. This entire procedure takes time O(k), where k was the total degree of inner vertices of P (this is because our cutting operation takes time proportional to the number of vertices of the near-drum we begin with, which is at most the complexity of P).

At every iteration, the complexity of P' is halved. Thus, if the initial complexity of P was O(n), then O(lg n) iterations are needed to reduce the complexity of P' to zero. If the complexity of P' is zero, then A_P(x) = 0 for all x. Thus, A(a) = A_P(a) + A_D(a) becomes A(a) = A_D(a). Thus, we can simply compute the maximum of A_D (which, recall, is a quadratic function) by computing its first derivative and equating it to 0. This will also give us the maximum of A.

At every iteration, when considering a near-drum P, we need O(k) time to find the median plane, O(k) time to compute the derivative of A_P at the median and O(k) time to perform our drum-cutting operation. Here, k is the complexity of P. Thus, the amount of work we do per iteration is O(k), that is, proportional to the complexity of P, which is halved at every iteration. This yields the familiar geometric series:

k + k/2 + k/4 + k/8 + ... -> 2k

Where k is the complexity of our initial near-drum P. Therefore, the total amount of work is bounded above by O(k), where k is the complexity of the polyhedron P we begin with. Since this is O(n), the entire algorithm runs in time O(n).

Wrapper Linear-MaxSecArea(K : convex polyhedron)

Find x = x₁ and x = x₂.

Let A_D be the zero function.

Let P be the convex near-drum defined by K and the planes x = x₁ and x = x₂.

If the planes x = x₁ and x = x₂ contain more than one vertex each, perform near-drum cutting on P and compute the quadratic area functions of the drums cut off P, accumulating them into A_D.

Run Linear-MaxSecArea(P, A_D).

Algorithm Linear-MaxSecArea(P : convex near-drum, A_D : real -> real)

If P is empty, compute A'_D, equate to zero and solve. Return the result.

Let x = x_m be the median plane between the supporting planes of P, x = x₁ and x = x₂. Construct a drum D between x_m and x_m + epsilon.

Compute A_P as a quadratic function between x_m and x_m + epsilon.

Compute p = A'_P(x_m).

Compute d = A'_D(x_m).

If p + d = 0, return x_m. If p + d < 0, let P' be the near-drum obtained by truncating P to the interval [x₁, x_m]. Let this new near-drum be P'. Perform near-drum cutting on P' and compute the quadratic area functions of the drums cut off P', accumulating them into A_D. Return Linear-MaxSecArea(P', A_D). If p + d > 0, let P' be the near-drum obtained by truncating P to the interval [x_m, x₂]. Continue as for the p + d < 0 case.

Note the near-drum cutting we do in the preprocessing phase. As mentioned earlier, to ensure that the complexity of our near-drum P is O(k) at every step, where k is the total degree of the inner vertices of P, we may have to do some cutting here, at the very beginning of the algorithm. However, since this cutting takes time O(n) and is done only once during preprocessing, the running time of the algorithm remains linear.

Note that we glossed over how to find the epsilon we use in our pseudocode. The most immediate way to do it would be to simply find the vertex that is closest, in x-coordinate, to x_m, and let epsilon be the x-distance between them (or less). Clearly, this step would take time proportional to the complexity of P, which, at this stage, is guaranteed to be O(k). Thus, this doesn't increase the asymptotic running time of the algorithm.

Next: Extensions.

Algorithms

O(n) time algorithm for convex drums

O(n2) time algorithm for convex polyhedra

O(n lg n) time algorithm for convex polyhedra

O(n) time algorithm for convex polyhedra

O(n²) time algorithm for convex polyhedra