Computing Maximum-Area Sections of Convex Polyhedra
Definitions
On this page, we'll give a number of definitions that will come in handy in presenting the required background. Feel free to skip this page or refer to it as needed if you're familiar with computational geometry in 3 dimensions.
Convex combination
Given n points x1, x2, ..., xn in any number of dimensions, a convex combination of these points is a sum of products a1x1 + a2x2 + ... + anxn, where 0 <= ai <= 1 for i = 1, 2, ..., n and a1 + a2 + ... + an = 1.
Convex hull in R3
In any number of dimensions, the convex hull of a set of points S can be defined in several ways:
- The smallest convex set containing all the points in S.
- The set of all convex combinations of the points in S.
- The intersection of all convex sets that contain all the points in S.
These definitions all hold in R3. We can also define the convex hull of two or more polygons or polyhedra using the same definitions as above, simply by considering our set S to be the set of vertices of the union of our polygons or polyhedra.
There are several useful informal ways to think of convex hulls:
- In R2, the convex hull of a set of points is the convex polygon obtained by stretching a rubber band around the points and letting it contract until it comes into contact with the "exterior" points.
- Analogously, in R3, the convex hull of a set of points is the convex polyhedron obtained by tightly stretching plastic wrap around the "exterior" points.
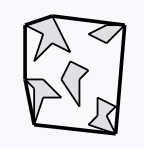
An example of the convex hull (bold) of several nonconvex polygons (shaded) in R2.
Convex polygon
A polygon P is convex if it is simple (noncrossing) and if for all points x, y in P, the closed line segment xy is also in P. In more graphic terms, a polygon is convex if its boundary has no dents or depressions, when viewed from the outside.
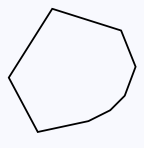
A convex polygon.
Convex polyhedron
A polyhedron K is convex if for all points x, y in K, the closed line segment xy is also in K. In more graphic terms, a polyhedron is convex if its boundary has no dents or depressions, when viewed from the outside.
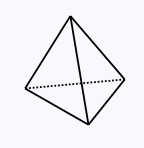
A convex polyhedron.
Drum
A polyhedron is a drum if all its vertices lie on two planes x = x1 and x = x2, both perpendicular to the x-axis. Note that drums can be convex or not.
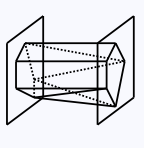
A drum.
Inner face
A face of a near-drum is an inner face if it is incident on an inner vertex.

Inner faces (shaded) incident on an inner vertex (circled).
Inner-face edge
An edge of a near-drum is an inner-face edge if it bounds an inner face.
Note that an inner-face edge can also be a long edge.
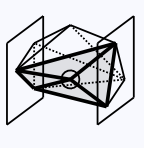
Inner-face edges (bold) bounding inner faces (shaded) incident on an inner vertex (circled).
Inner vertex
A vertex of a near-drum between the planes x = x1 and x = x2 is an inner vertex if it lies strictly between the planes x = x1 and x = x2.
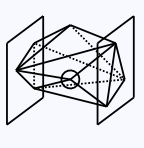
An inner vertex (circled).
Long edge
An edge of a near-drum between planes x = x1 and x = x2 is a long edge if its endpoints are not both in either x = x1 or x = x2 and neither of its endpoints is an inner vertex.
In other words, an edge of a near-drum between planes x = x1 and x = x2 is a long edge if one of its endpoints is in the plane x = x1 and the other is in the plane x = x2.
Note that a long edge can also be an inner-face edge.
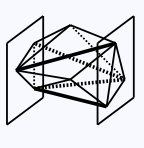
Long edges (bold).
Minkowski addition in R2
Minkowski addition allows us to sum various shapes in R2. Although it is defined for any number of dimensions, only the case of R2 will be of interest to us. In particular, we will be interested in summing convex polygons. Note, however, that Minkowski addition in R2 is defined, as follows, for any two sets in R2: Given two sets A and B in R2, their sum, A + B, is obtained by adding each element of A to each element of B. This is a rather terse definition and there are more visual ways of thinking about it.
Minkowski addition is sometimes called vector addition, since we can consider sets of points in R2 (or, indeed, any number of dimensions) as sets of vectors: With each point p in a set P, we associate, through some policy, a unique vector <p>. For instance, <p> could be the vector from the origin to the point p. This guarantees a one-to-one correspondence between points and vectors. Then, adding two sets simply becomes vector addition over all the vectors associated with points in the two sets.
Formally, A + B = C if and only if for every point c in C, there exist points a in A and b in B such that <a> + <b> = <c>, where the angle brackets denote our point-to-vector encoding.
See Alexander Bogomolny's page on Minkowski addition for an interesting interactive Java applet demonstrating Minkowski addition in R2.
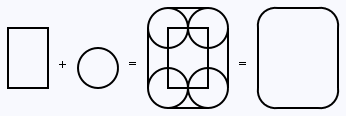
An example of summing two sets in R2.
Monotonicity
A function f from the reals to the reals is monotonically increasing if for any reals x, y, if x <= y, then f(x) <= f(y). A function f is monotonically decreasing if for any reals x, y, if x <= y, then f(x) >= f(y).
A function f is strictly monotonically increasing or strictly monotonically decreasing if the above inequalities are strict.
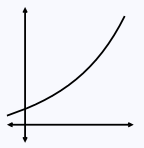
A plot of a strictly monotonically increasing function.
Near-drum
A polyhedron is a near-drum if all its vertices lie between two planes x = x1 and x = x2, both perpendicular to the x-axis. Note that all drums are also near-drums and that near-drums can be convex or not.
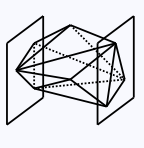
A near-drum.
Plane
A plane is an infinite, 2-dimensional object, an infinitely large sheet of paper. We will show planes as finite sheets, bounded by rectangles or other polygons.
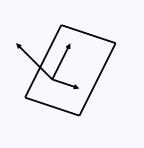
A plane, including surface and normal vectors.
Polygon
A polygon is a 2-dimensional region of space defined by a finite sequence of line segments such that any two line segments adjacent in the sequence share an endpoint. These line segments define the boundary of the polygon and are usually called edges. The points where adjacent edges meet are usually called vertices. Usually, a polygon is given by a list of the Cartesian coordinates of its vertices in traversal order.
A polygon is simple if it is noncrossing, that is, if any two nonadjacent edges do not meet anywhere, and any two adjacent edges meet only at their shared endpoint. We will be concerned mainly with simple polygons and will usually omit the modifier.
Note that a simple polygon separates the plane it is in into two regions: the bounded interior and the unbounded exterior. Polygons can be convex or not.
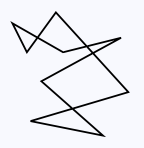
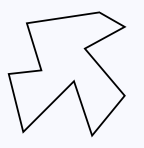
A nonconvex nonsimple polygon (left) and a nonconvex simple polygon (right).
Polyhedron
A polyhedron is a 3-dimensional region of space defined by a finite number of polygonal faces which meet at edges, which, in turn, meet at vertices. Exactly two faces are incident on every edge, while at least three faces are incident on every vertex. A polyhedron is the natural extension of a polygon in 3 dimensions.
Polyhedra can be represented using a number of standard data structures, one of the oldest and most popular of which is the winged-edge data structure. We will assume that our polyhedra are represented using this data structure. In the winged-edge, each edge e carries eight pointers: two to the endpoints of e, v0 and v1; two to the faces that e bounds, f0 to the left of v0v1 and f1 to the right of v0v1; and four to the "wings" of e. The wings of e are the predecessors and successors of e when traversing its faces f0 and f1 in the direction indicated by v0v1. For more information, see [2] or Prof Ching-Kuang Shene's notes on the winged-edge.
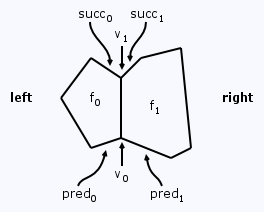
The pointers associated with an edge e in the winged-edge data structure for representing polyhedra.
We will not be using the properties of the winged-edge much. However, it will come in handy when considering the running times of the algorithms we will look at.
Note that a polyhedron separates the space it is in into two regions: the bounded interior and the unbounded exterior. Polyhedra can also be convex or not. Furthermore, if a polyhedron is convex, then all of its faces must be convex polygons.
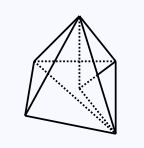
A nonconvex polyhedron.
Unimodal function
A function f from the reals to the reals is unimodal if for some real nonempty closed interval [m1, m2] (it could be that m1 = m2), f(x) is monotonically increasing for x <= m1, monotonically decreasing for x >= m2 and f(x) = f(m1) = f(m2) for x in [m1, m2]. Thus, [m1, m2] can be considered a global maximum region of f. Note that unimodal functions also include functions that are monotonically decreasing before m1 and monotonically increasing after m2, in which case [m1, m2] is a global minimum region of f. However, we will mainly be interested in the case of [m1, m2] being a maximum, rather than a minimum, and this is what we will mean by a function being unimodal.
A function f is strictly unimodal if the increases and decreases before and after [m1, m2] are strictly monotonic.
Observe that an alternative definition of strict unimodality is as follows: A function f from the reals to the reals is strictly unimodal if for all reals x, y such that x < y, the value w = min{f(x), f(y)} is either the global maximum (or minimum) of f, or w < f(z) for all z in the open interval (x, y).
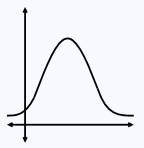
A plot of a unimodal function (here, m1 = m2).
Scalar multiplication of sets in R2
We will be interested in the idea of multiplying a polygon P by a scalar s. How can we think of this? In Minkowski addition, we associated, with each point of our set in R2, a unique vector. Here, we can do the same. For each point p in P, let us define a unique vector <p> (see Minkowski addition for an example encoding).
Now, to obtain Q = sP, the product of polygon P and scalar s, we multiply every vector associated with a point in P by the scalar s. This will give a collection of vectors that define the points of Q. Formally, Q = sP if and only if for every point q in Q, there exists a point p in P such that <q> = s<p>, where the angle brackets denote our point-to-vector encoding.
Note that this scalar multiplication is better known simply as "scaling". We are enlarging or shrinking our polygon. However, we define it in this involved way as an operation related to Minkowski addition. Note also that this approach can be used for any set of points in any number of dimensions. However, we will use it primarily with convex polygons in R2.
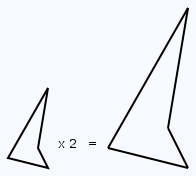
An example of multiplying a nonconvex polygon by a scalar.
Sectional area function
Let K be a polyhedron. Let p(a) be the plane x = a. The sectional area function of K, denoted A(a), is the area of the polygonal section obtained by intersecting K with the plane p(a).
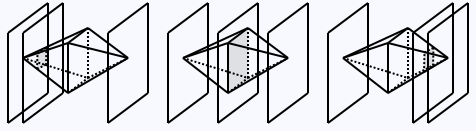
The values of A(a) for several values of a are the areas of the sections (shaded).
Section of a polyhedron
A section of a polyhedron K is the intersection between K and some plane p. Generally, we assume sections to be nonempty, that is, we assume that p actually meets K somewhere.
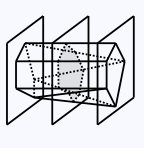
A section (shaded) of a polyhedron (here, a drum).
Supporting plane
A supporting plane p of a polyhedron K is a plane that passes through at least one vertex of K such that every point of K lies either on p or on one side of p.
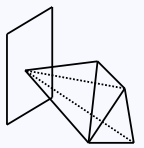
A supporting plane of a polyhedron.
Next: Background.