Computing Maximum-Area Sections of Convex Polyhedra
Background
Now, let's build up the background needed to understand the algorithms we'll look at to solve the problem at hand. Although some of the material here may appear dense at first, all of it will, rest assured, come in handy.
In between the main results, we may have some links to the algorithms that actually use them.
The unimodality of the sectional area of convex polyhedra
In this section, we'll let K be a convex polyhedron and A(a) the sectional area function of K. That is, A(a) is the area of the section obtained by intersecting K with the plane x = a. In building algorithms to solve the maximum-area section problem for convex polyhedra, we'll need the following famous result, known as the Brunn-Minkowski theorem or the Brunn-Minkowski inequality:
Theorem (Brunn-Minkowski in R2): If P and Q are convex polygons and Area(P) denotes the area of a polygon P, then for any 0 < q < 1,
(Area(qP + (1-q)Q))1/2 >= q(Area(P))1/2 + (1-q)(Area(Q))1/2.On the left hand side, + denotes Minkowski addition of polygons and multiplication involves products of scalars and polygons. Equality holds if and only if P and Q are homothetic, that is, if there exist a q > 0 and a p in R2 such that Q = qP + p.
We'll use this result without proof. For more information on the Brunn-Minkowski theorem (such as a proof), see [3] or Prof Santosh Vempala's notes on the Brunn-Minkowski inequality. The case of equality doesn't concern us here, so whether or not our polygons are homothetic doesn't really matter. We will simply use the theorem as given.
We will also use the following result, which we will prove:
Lemma (containment): Let K be a convex polyhedron with sectional area function A(a). Let P1 be the polygonal section obtained by intersecting K with some plane x = x1. Let P2 be the polygonal section obtained by intersecting K with some plane x = x2, where x1 < x2. Let Area(P) denote the area of a polygon P. Then for any 0 <= q <= 1,
A(qx1 + (1-q)x2) >= Area(qP1 + (1-q)P2).On the right hand side, + denotes Minkowski addition of polygons and multiplication involves products of scalars and polygons.
Proof: By contradiction, we will show that the polygonal section obtained by intersecting K with x = qx1 + (1-q)x2 contains the polygon qP1 + (1-q)P2. Suppose that this polygonal section does not contain the polygon qP1 + (1-q)P2. Consider the 3-dimensional convex hull C of the union of P1 and P2. P1 and P2 are polygons in R3, contained in two planes x = x1 and x = x2, both parallel to the x-axis. Thus, C is a drum between the planes x = x1 and x = x2. Furthermore, by one definition of the convex hull, any convex combination of P1 and P2, that is, qP1 + (1-q)P2 for 0 <= q <= 1, lies within C. In particular, any convex combination of P1 and P2 is a section of C, in the plane x = qx1 + (1-q)x2. Since K is a convex polyhedron containing P1 and P2 and C is the smallest convex polyhedron containing P1 and P2, K must be a superset of C. If the polygonal section of K intersected with x = qx1 + (1-q)x2 does not contain the polygon qP1 + (1-q)P2, then K cannot be a superset of C, contradicting our previous observation.
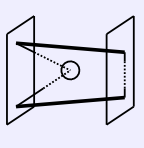
The drum formed between P1 and P2 is their convex hull and thus contains every convex combination of P1 and P2, that is, every polygon qP1 + (1-q)P2 for 0 <= q <= 1. Polyhedron K (hinted at by dashed lines), being convex, must be at least as large as this convex hull, as it also contains both P1 and P2.Thus, it must be that the polygonal section of K intersected with x = qx1 + (1-q)x2 contains the polygon qP1 + (1-q)P2, from which it follows that A(qx1 + (1-q)x2) >= Area(qP1 + (1-q)P2) for 0 <= q <= 1. QED.
Armed with these results, we can now begin proving that the sectional area function of a convex polyhedron is unimodal, an important fact. First, however, let's look at a fairly straightforward little lemma.
Lemma (unimodality): The sectional area function A(a) of a convex polyhedron K is a strictly unimodal function if, for any open interval X = (x1, x2), mina in X A(a) = min{A(x1), A(x2)}.
Proof: Recall that one formulation of strict unimodality is as follows: A function f from R to R is strictly unimodal with a single maximum region if for any x1, x2 in R such that x1 < x2, the value w = min{f(x1), f(x2)} is either the global maximum of f, or w < f(z) for all z in the open interval (x1, x2). Thus, if, for any open interval X = (x1, x2), mina in X A(a) = min{A(x1), A(x2)}, then from our alternative formulation of strict unimodality above, it follows immediately that the function A(a) is strictly unimodal on every interval, from which it follows that it is unimodal on an interval containing the whole of K. QED.
At last, we are able to prove the main result of this section:
Theorem (unimodality of sectional area of convex polyhedra): The sectional area function A(a) of a convex polyhedron K is a strictly unimodal function.
Proof: We will show that for any open interval X = (x1, x2), it is the case that mina in X A(a) = min{A(x1), A(x2)}. By the unimodality lemma, it will then follow that A(a) is a strictly unimodal function.
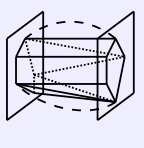
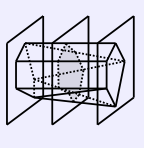
Several sections of a convex polyhedron. Intuitively, the strict unimodality of the sectional area function A seems obvious.Consider an arbitrary open interval X = (x1, x2). Suppose, without loss of generality, that A(x1) >= A(x2). Observe that any x in X can be expressed as qx1 + (1-q)x2 for 0 < q < 1. Now, let P1 be the polygonal section obtained by intersecting K with the plane x = x1 and let P2 be the polygonal section obtained by intersecting K with the plane x = x2. If either one of these two polygons, P1 or P2, is empty, then either A(x1) = 0 or A(x2) = 0. Either way, this means that min{A(x1), A(x2)} = 0, since A(x) >= 0 for all x. This means that mina in X A(a) = 0 = min{A(x1), A(x2)}. So let us suppose that P1 and P1 are both nonempty.
Because K is convex, we know that both P1 and P1 must be convex. Why? By contrapositive, if either of P1 or P2 would be nonconvex, then it would be obvious that K, too, would be nonconvex. Now, by the containment lemma, we know that for any 0 < q < 1, the intersection of K with the plane qx1 + (1-q)x2 contains the polygon qP1 + (1-q)P2. Thus, we know that (A(qx1 + (1-q)x2))1/2 >= (Area(qP1 + (1-q)P2))1/2.
We can now use the Brunn-Minkowski theorem in R2 on the right hand side of this inequality to see that (Area(qP1 + (1-q)P2))1/2 >= q(Area(P1))1/2 + (1-q)(Area(P2))1/2. Manipulating the right hand side of this inequality reveals that q(Area(P1))1/2 + (1-q)(Area(P2))1/2 = (Area(P2))1/2 + q((Area(P1))1/2 - (Area(P2))1/2)
Combining these inequalities and observations, we obtain that (A(qx1 + (1-q)x2))1/2 >= (Area(P2))1/2 + q((Area(P1))1/2 - (Area(P2))1/2).
Recall that we are assuming that A(x1) >= A(x2). This means that Area(P1) >= Area(P2), which means that (Area(P1))1/2 >= (Area(P2))1/2. We also know that 0 < q < 1. Why does this matter? It matters because it shows us that q((Area(P1))1/2 - (Area(P2))1/2) must be nonnegative. Thus, we can drop it from the inequality obtained in the previous paragraph, yielding the following: (A(qx1 + (1-q)x2))1/2 >= (Area(P2))1/2. Plugging in the fact that x = qx1 + (1-q)x2, this produces (A(x))1/2 >= (Area(P2))1/2, from which A(x) >= A(x2) follows immediately. This holds for every x in the interval (x1, x2).
Thus, mina in X A(a) = A(x2). If we had started with the assumption A(x2) >= A(x1), we would have obtained mina in X A(a) = A(x1). Either way, it is the case that mina in X A(a) = min{A(x1), A(x2)}. Thus, by the unimodality lemma, the function A(a) is strictly unimodal. QED.
This is an important result which we will use in all of our algorithms. In particular, note that the unimodality of sectional area of convex polyhedra allows us to apply a divide-and-conquer approach in searching for the plane that yields the maximum-area section. This is exactly what we do in several of the algorithms we will look at. The algorithm BinarySearch-MaxSecArea, for instance, exploits this property, as does our implementation in the applet.
For now, however, let's go on with a little more theory.
The quadratic sectional area of drums
We say that a polyhedron P is a drum if all of its vertices lie only in two planes x = x1 and x = x2, both perpendicular to the x-axis.
Theorem (quadratic sectional area of drums): Let K be a drum with vertices on planes x = x1 and x = x2, with x1 < x2. Then A(a) is a quadratic function for x1 <= a <= x2.
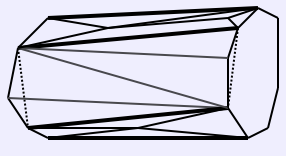
Proof: Any x1 <= a <= x2 can be expressed as qx1 + (1-q)x2 for 0 <= q <= 1. The polygonal section of K intersected with plane x = qx1 + (1-q)x2 for some q is a simple polygon P with vertices p1, p2, ..., pn. Every vertex pi can be expressed in terms of its Cartesian coordinates as (pix, piy, piz).
Slicing through a drum.Recall that the signed area A(P) of P is given by
A(P) = (1/2) Sum1<=i<=n (pi-1ypiz - pi-1zpiy).(For more information on this formula, including a proof, see [2].) Now, observe that every vertex pi is the point of intersection between the plane x = qx1 + (1-q)x2 and some edge of K. Since K is a drum, one of the endpoints of this edge is on the plane x = x1 and the other is on the plane x = x2. Let the endpoint on the plane x = x1 be vi and let the endpoint on the plane x = x2 be wi. Then pi = qvi + (1-q)wi. Expanding this into Cartesian coordinates, piy = qviy + (1-q)wiy and piz = qviz + (1-q)wiz. Recall that thoughout all of this, we are holding q fixed. Substituting these expansions into the expression for area A(P), we obtain a function that is quadratic in q, since vi and wi are determined by pi. Let us perform this substitution and see what our quadratic sectional area function looks like. Doing this yields the extremely ugly quadratic function
A(P) = (1/2) Sum1<=i<=n (q2(vi-1yviz - vi-1ywiz - wi-1yviz + wi-1ywiz - vi-1zviy + wi-1zviy - wi-1zwiy + vi-1zwiy) + q(vi-1ywiz + wi-1yviz - 2wi-1ywiz - vi-1zwiy - wi-1zviy + 2wi-1zwiy) + (wi-1ywiz-wi-1zwiy)).(Don't worry, we won't be using this expression much.)
Since we defined P to be the polygonal section of K intersected with plane x = qx1 + (1-q)x2, this means that the area function A(a) itself is quadratic in a, since a linearly determines q. QED.
Already at this stage, we can observe that any convex polyhedron K can be decomposed into O(n) drums, simply by passing planes perpendicular to the x-axis through every vertex. Since there are n vertices, this gives O(n) planes, where, if we let the intersection of a plane and an edge of K be a new point, every interval between adjacent planes is a drum. Thus, we obtain O(n) drums. However, every drum in this decomposition can have O(n) vertices (one new vertex for every edge that the planes slice through), resulting in a worst case total of O(n2) vertices in our resulting decomposition. Nevertheless, we will be using this result in several of the algorithms, such as Drum-MaxSecArea, Quadratic-MaxSecArea and BinarySearch-MaxSecArea.
In fact, the results we've covered up to now are sufficient to construct an O(n lg n) time algorithm for arbitrary convex polyhedra (such as BinarySearch-MaxSecArea). However, to reach O(n) time, we need a smarter approach and more theory.
(Fear not, this will be the last result we will prove. After this, we'll be looking at what we can do with all this knowledge.)
Decomposing convex near-drums into drums and a smaller near-drum
A near-drum is a polyhedron whose vertices all lie between two planes x = x1 and x = x2. Clearly, every convex polyhedron is a convex near-drum. We can simply let the supporting planes of the x-extremal vertices that are perpendicular to the x-axis be the planes x = x1 and x = x2.
In this section, we will show that every convex near-drum K with n vertices, whose inner vertices have total degree k, can, in O(n) time, be decomposed into a set of drums (possibly nonconvex) with O(n) vertices in total, leaving behind a single convex near-drum with O(k) vertices. As we will see on the algorithms page, this linear time decomposition will be crucial in our linear time algorithm for finding the maximum-area section of a convex polyhedron. We will effectively keep decomposing our near-drum, making sure its complexity decreases sufficiently quickly. But more on this later.
Theorem (near-drum decomposition): Let K be an n-vertex near-drum with all vertices between planes x = x1 and x = x2, with x1 < x2. Let K's inner vertices have total degree k. In O(n) time, we can decompose K into a set of drums with O(n) vertices in total, leaving a single convex near-drum with O(k) vertices.
Proof: We will show how to cut off drums from our near-drum, such that O(k) cutting operations are needed to reduce our n-vertex near-drum to one with O(k) vertices. The total running time will be dominated by an O(n) term caused by some initial preprocessing. Furthermore, we will show that since every edge in K can be cut off into a drum at most once, the resulting drums will have O(n) edges and thus O(n) vertices in total.
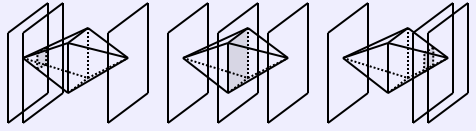
Consider an inner vertex of K. If K has no inner vertices, it is a drum with O(n) vertices, so our decomposition is finished already. So let's suppose that K has at least one inner vertex v. Then at least 3 inner faces meet at v. These inner faces are bounded by inner-face edges. Consider the set of all inner-face edges of a convex near-drum K.
Some inner-face edges (bold) of a convex near-drum.
The inner faces these edges bound are shaded, the inner vertex these faces are incident on is circled.Each inner face is bounded by at most one long edge. Why? Suppose an inner face were bounded by, say, two long edges. Since it is an inner face, it must also be bounded by edges incident on an inner vertex. From the following diagram, it is easy to see that this can only occur if the inner face is nonconvex:
If an inner face is bounded by two long edges (bold), it must be nonconvex. The inner vertex is circled.However, our near-drum K is convex, so all of its faces must be convex. Therefore, an inner face can be bounded by at most one long edge.
Now, let's count the number of inner-face edges. If an inner vertex v has degree j, then exactly j inner faces are incident on it. As we observed above, each of these inner faces can be bounded by at most one long edge. If the total degree of all inner vertices is k, this contributes at most k inner-face edges that are also long-edges. Clearly, the remaining inner-face edges are those edges that are not long edges but are incident on inner vertices. If the total degree of all inner vertices is k, then we have an immediate upper bound of k inner-face edges that are incident on inner vertices. Thus, adding this to the k inner-face edges that are also long edges, there are at most 2k inner-face edges in our near-drum K.
Note that if all edges of K are inner-face edges, then our decomposition is already finished, since we have a convex near-drum with O(k) vertices. So let's suppose that not all edges of K are inner-face edges.
By searching over those edges of K that are not inner-face edges, we must find a drum that we can cut off K. Observe that if an edge of K is not an inner-face edge, it must either be a long edge or lie completely in one of the planes x = x1 or x = x2. If K has no long edges that are not inner-face edges (that is, all of K's long edges are also inner-face edges), then all edges, except for those that lie completely in the planes x = x1 and x = x2 are inner-face edges. Recall that there are at most 2k such edges. Each edge has two endpoints, so this tells us that there are at most 4k vertices that are endpoints of inner-face edges. If a vertex v lies in one of the two planes x = x1 and x = x2 and all long edges are inner-face edges, then there must be at least one inner-face edge which is incident on v. Why? If a vertex in one of the two planes x = x1 and x = x2 belongs to only edges in these planes, it can be deleted without affecting K. Thus, our upper bound of 4k vertices includes all vertices of the near-drum. This means that our decomposition is complete, since we have a convex near-drum with O(k) vertices. So let's assume that not all long edges are inner-face edges.
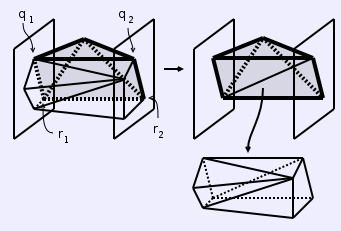
Consider a sequence of long edges that are not inner-face edges but that lie between long edges that are inner-face edges. What does this mean? Consider ordering the long edges of K around K's axis: e1, e2, ..., em. In this ordering, some of the ei's will be inner-face edges. Pick a sequence of long edges that are not inner-face edges such that the two long edges before and after the sequence are inner-face edges.
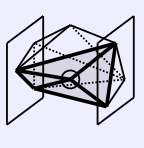
Finding a sequence of long edges that are not inner-face edges. The edges in bold are long edges that are also inner-face edges. The edges in grey are a sequence of long edges that are not inner-face edges, but are bounded by long edges that are inner-face edges. The dotted lines indicate where we will cut.Let the inner-face long edges that bound our sequence be (q1, q2) and (r1, r2), where q1 and r1 lie in the plane x = x1 and q2 and r2 in the plane x = x2 . Now, things get exciting. Consider cutting along the boundary of the quadrilateral (q1, q2, r2, r1). This will cut off part of the surface of K. Call this cut off part D and let the remaining part be the new K. D has no inner vertices, since it is defined exclusively by long edges and none of the long edges of D are inner-face edges. Even the added edges, (q1, q2) and (r1, r2), are not inner-face edges on D, since the inner vertices they were incident on remain in K (otherwise, more of the long edges now in D would have been inner-face edges when part of K before the cutting). Since D has no inner vertices, it must be a drum:
Cutting off a drum. Note the added diagonal.Note that in the diagram above, we added a diagonal across the quadrilateral (q1, q2, r2, r1). Recall that we must ensure that our near-drum remains convex. The outside of the near-drum is still convex, since we did nothing to it, but the surface of the quadrilateral we cut along may be nonconvex. To avoid this problem, we let our new near-drum K be the convex hull of our cut near-drum. This adds at most one diagonal. It might add none. It might be that the quadrilateral (q1, q2, r2, r1) lies in a plane, in which case no diagonals are needed. In any case, if we do add a diagonal, we must add the same diagonal to the severed part D to guarantee that it is still, in fact, a legal polyhedron. Moreover, after this fix, we know that D must be a drum. Note that D may or may not be convex.
Note also that although we say that we let our new near-drum K be the convex hull of the cut near-drum, we need not actually compute the convex hull. We must simply test the planarity properties of the four vertices of the quadrilateral (q1, q2, r2, r1) to see which, if any, diagonal must be added. This test breaks down into a number of cases that can easily be implemented in constant time.
We can repeat the above drum-cutting procedure on all sequences of long edges of K that are not inner-face edges. Every inner face can be bounded by at most one long edge. Every inner vertex v defines deg(v) inner faces, where deg(v) is the degree of v. So there can be at most k long edges that are inner-face edges. Thus, there can be at most k sequences of long edges of K that are not inner-face edges (those sequences of long edges that occur in between long edges that are also inner-face edges). This means that we can carry out the drum-cutting operation at most O(k) times. Note that we cannot cut off more than O(n) edges from our original near-drum, so the total edges and vertices of the obtained drums cannot exceed O(n). If no more cutting operations can be carried out on the final near-drum, all of its long edges are inner-face edges, of which there are at most 2k. By a similar argument as used above, this means that there are O(k) vertices in our final near-drum.
As for the running time, we know that we can perform at most O(k) cutting operations, where each cutting operation takes constant time. We can, in O(n) time, traverse K to find all sequences of long edges that are not inner-face edges. There is no need to explicitly sort the long edges around K, since traversing the "end-polygons" in the planes x = x1 and x = x2 gives us the long edge ordering. We are able to do this, assuming our near-drum is stored in a standard data structure, such as a winged-edge. This need only be done once. Afterwards, each cutting operation only requires constant time updates to our list of remaining long edge sequences that are not inner-face edges. Thus, the running time is dominated by O(n). Also, it could be that k is O(n), if almost all of our near-drums vertices are inner-vertices. In any case, we obtain an O(n) running time. QED.
It's now time to roll up our sleeves and see what we can do with these results. We will see several algorithms and algorithm outlines of varying time complexities, culminating in the linear time algorithm that requires all this heavy background.
Next: Algorithms.