

Next: Kernel Basis Functions
Up: svkde
Previous: Non-Parametric Density Estimation
In the previous section we decomposed the CDF into regions or windows
 and estimated the PDF for each window separately. There are several ways to choose the placement (i.e. the center) of the windows; for example they can be disjoint and cover the entire domain as is the case with Frequency Histogram Estimation (Figure 2); the benefit of using such a method is that the structure of the windows are independant of the number of random samples (although the estimation procedure is not). Alternatively, the approach we will consider henceforth will associate a window with each random sample
and estimated the PDF for each window separately. There are several ways to choose the placement (i.e. the center) of the windows; for example they can be disjoint and cover the entire domain as is the case with Frequency Histogram Estimation (Figure 2); the benefit of using such a method is that the structure of the windows are independant of the number of random samples (although the estimation procedure is not). Alternatively, the approach we will consider henceforth will associate a window with each random sample 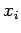 so that we have a sequence of windows
so that we have a sequence of windows
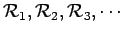 centered at
centered at
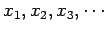 . Since the number of windows (and their volume) is now dependent on the sample size we will re-write the result (5) as
. Since the number of windows (and their volume) is now dependent on the sample size we will re-write the result (5) as
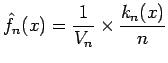 |
(6) |
where 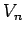 is the volume of the region
is the volume of the region
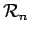 and
and 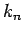 is the number of samples that fall inside it; as more samples are generated the regions can either be refined (as is the case with the Parzen method) or we can reverse this logic and gradually increase the size of the regions starting with an inconspicuously small
is the number of samples that fall inside it; as more samples are generated the regions can either be refined (as is the case with the Parzen method) or we can reverse this logic and gradually increase the size of the regions starting with an inconspicuously small
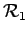 (which is the case with the nearest-neighbor estimation method).
(which is the case with the nearest-neighbor estimation method).
Let us further generalize [DHS01] the definition of the region
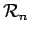 so that we can estimate multi-variate densities; assume the windows
so that we can estimate multi-variate densities; assume the windows
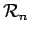 are d-dimensional hypercubes with edges of length
are d-dimensional hypercubes with edges of length 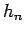 ; the volume is then simply
; the volume is then simply
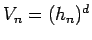 .
.
Figure:
Let the hypercube window
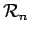 have dimension
have dimension 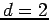 ; then
; then 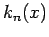 is simply a count of the random samples that fall in the square with sides of length
is simply a count of the random samples that fall in the square with sides of length 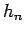 and centered at
and centered at 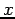 ; in this case
; in this case 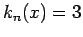 .
.
|
|
Now that the window has changed we need to revise our definition of 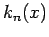 which was previously defined using a simple indicator function
which was previously defined using a simple indicator function
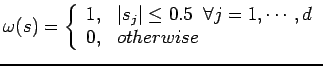
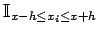 ; generalising this from counting random samples within an interval to counting within a hypercube can be done by first using a window function
; generalising this from counting random samples within an interval to counting within a hypercube can be done by first using a window function 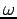 of the form:
which defines the boundary for a unit-hypercube centered at the origin and then defining
of the form:
which defines the boundary for a unit-hypercube centered at the origin and then defining 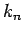 as follows:
So
as follows:
So
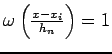 if and only if
if and only if
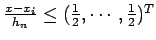 or
or
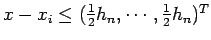 , in other words if
, in other words if 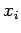 is less than half the length of an edge of the hypercube away from
is less than half the length of an edge of the hypercube away from 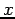 in all dimensions
in all dimensions
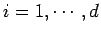 . So
. So
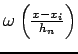 defines a (d+1)-dimensional hypercube of volume
defines a (d+1)-dimensional hypercube of volume 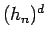 (since the (d+1)th dimension has edges of length
(since the (d+1)th dimension has edges of length 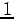 ), centered at
), centered at 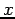 which counts the number of random samples that fall within the d-dimensional hypercube window
which counts the number of random samples that fall within the d-dimensional hypercube window
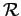 . Finally substituting this result into 6 gives:
. Finally substituting this result into 6 gives:
The resulting estimated density is `jagged' since the window (basis) functions in the above linear combination are hypercubes (Figure 3) with abrupt edges; reducing the width 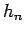 as more samples are generated will smooth out the estimate. Infact if
as more samples are generated will smooth out the estimate. Infact if
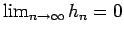 then the estimated density function is proved [Fuk72] to be asymptotically unbiased;
then the estimated density function is proved [Fuk72] to be asymptotically unbiased;
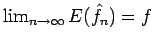 .
.
Subsections


Next: Kernel Basis Functions
Up: svkde
Previous: Non-Parametric Density Estimation
Rohan Shiloh SHAH
2006-12-12
![]() and estimated the PDF for each window separately. There are several ways to choose the placement (i.e. the center) of the windows; for example they can be disjoint and cover the entire domain as is the case with Frequency Histogram Estimation (Figure 2); the benefit of using such a method is that the structure of the windows are independant of the number of random samples (although the estimation procedure is not). Alternatively, the approach we will consider henceforth will associate a window with each random sample
and estimated the PDF for each window separately. There are several ways to choose the placement (i.e. the center) of the windows; for example they can be disjoint and cover the entire domain as is the case with Frequency Histogram Estimation (Figure 2); the benefit of using such a method is that the structure of the windows are independant of the number of random samples (although the estimation procedure is not). Alternatively, the approach we will consider henceforth will associate a window with each random sample ![]() so that we have a sequence of windows
so that we have a sequence of windows
![]() centered at
centered at
![]() . Since the number of windows (and their volume) is now dependent on the sample size we will re-write the result (5) as
. Since the number of windows (and their volume) is now dependent on the sample size we will re-write the result (5) as
![]() so that we can estimate multi-variate densities; assume the windows
so that we can estimate multi-variate densities; assume the windows
![]() are d-dimensional hypercubes with edges of length
are d-dimensional hypercubes with edges of length ![]() ; the volume is then simply
; the volume is then simply
![]() .
.
![\includegraphics[scale=1.25]{image_hypercube_window_function.eps}](img86.png)
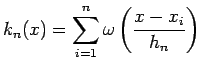
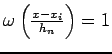 if and only if
if and only if
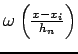 defines a (d+1)-dimensional hypercube of volume
defines a (d+1)-dimensional hypercube of volume