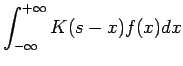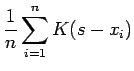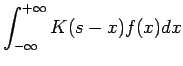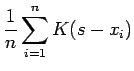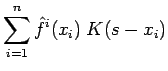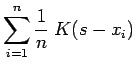

Next: Bandwidth Matrix Selection
Up: Kernel Density Estimation: Parzen
Previous: Kernel Basis Functions
The estimate 8 can be re-written as a convolution of the kernel with the true density function;
and so in a sense, the kernel density estimate is approximately a deconvolution from the true density; in [DH73] we see that in the limit as the number of random samples approaches infinity,
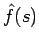 converges to
converges to
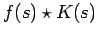 . We can also write the density estimate as a smoothing (we refer to smooth and smoothing in two contexts; smooth functions have continuous derivatives and smoothing operations remove localized features) convolution of the impulsive density function (which assigns a probability mass of
. We can also write the density estimate as a smoothing (we refer to smooth and smoothing in two contexts; smooth functions have continuous derivatives and smoothing operations remove localized features) convolution of the impulsive density function (which assigns a probability mass of
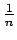 to each of the
to each of the 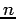 random samples;
random samples;
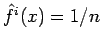 ) with the kernel function:
) with the kernel function:
Essentially the convolution is a regularization of the estimate through the addition of `smoothing' noise in the regions where the impulsive density is undefined.
It is interesting to note that the Parzen Method has been shown [ZPR05] to be equivalent to a Regularized Least Squares Method (or Tikhonov Regularization) where the regularizing functional is taken to be the norm of the resulting estimated density. One benefit [MZ00] of `regularizing by convolving' is that there are no explicit regularization parameters that need to be estimated and then re-trained.


Next: Bandwidth Matrix Selection
Up: Kernel Density Estimation: Parzen
Previous: Kernel Basis Functions
Rohan Shiloh SHAH
2006-12-12