

Next: Kernel Density Estimation: Parzen
Up: svkde
Previous: svkde
Provided with 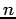 discrete observations of a random variable
all of which are identically and independently distributed (iid) according to some unknown probability distribution
discrete observations of a random variable
all of which are identically and independently distributed (iid) according to some unknown probability distribution 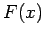 , we seek an estimate
, we seek an estimate
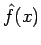 of the true probability density function
of the true probability density function 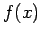 . The search for
. The search for
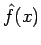 is usually performed in a restricted functional space
is usually performed in a restricted functional space
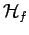 ; which is infact a Reproducing Kernel Hilbert Space (see Section
; which is infact a Reproducing Kernel Hilbert Space (see Section ![[*]](file:/usr/local/share/latex2html/icons/crossref.png) ). The functional space is further restricted to only those functions that are non-negative and integrate to one. The probability density function (PDF) is simply the derivative of the cumulative distribution function (CDF):
). The functional space is further restricted to only those functions that are non-negative and integrate to one. The probability density function (PDF) is simply the derivative of the cumulative distribution function (CDF):
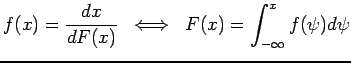 |
(2) |
We can rewrite 2 as a linear mapping [WGS+99]:
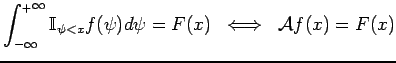 |
(3) |
where both integrals in 2 and 3 are vector integrations and
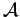 is an injective mapping from
is an injective mapping from
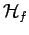 to the Hilbert Space where
to the Hilbert Space where 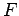 is defined;
is defined;
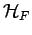 . Neither
. Neither 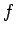 or
or 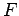 are known (whereas the operator
are known (whereas the operator
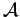 and its inverse are well defined) so we begin by estimating
and its inverse are well defined) so we begin by estimating 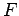 using samples
using samples
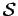 generated by the random process and then proceed to deriving
generated by the random process and then proceed to deriving 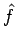 from our estimate
from our estimate 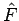 using an approximation of the inverse of the linear transformation
using an approximation of the inverse of the linear transformation
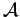 .
.
The empirical distribution at 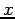 can be estimated from the data by taking the ratio of the number of samples that are less than or equal to
can be estimated from the data by taking the ratio of the number of samples that are less than or equal to 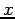 to the total number of samples:
to the total number of samples:
![$\displaystyle \hat{F}(x) = \frac{1}{n}\sum_{i=1}^n \mathbb{I}_{( -\infty, \; x_i]} (x)$](img45.png) |
(4) |
and is an unbiased maximum likelihood estimate that is piece-wise constant. For the density to exist, the estimated distribution 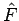 must be differentiable and hence continuous and so to smooth out the estimate
must be differentiable and hence continuous and so to smooth out the estimate 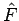 ; a non-linear regression (Figure 1) is used to approximate the distribution in the regions where training samples are unavailable; specifically the regression is performed on the set of pairs
and is parametrized by the vector
; a non-linear regression (Figure 1) is used to approximate the distribution in the regions where training samples are unavailable; specifically the regression is performed on the set of pairs
and is parametrized by the vector 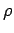 which leads to our new estimate for the distribution:
which leads to our new estimate for the distribution:
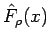 . Support Vector Regression techniques may also be used to derive accurate regressions since regularization (see Section
. Support Vector Regression techniques may also be used to derive accurate regressions since regularization (see Section ![[*]](file:/usr/local/share/latex2html/icons/crossref.png) ) is then possible.
) is then possible.
Now to estimate the density function at 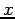 we need to estimate the derivative of
we need to estimate the derivative of
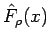 which can roughly be done by taking the difference between two evaluations of the distribution function at fixed lengths
which can roughly be done by taking the difference between two evaluations of the distribution function at fixed lengths 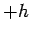 and
and 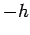 from
from 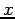 :
:
Figure:
Estimating the Density and Distribution Functions: [left] A linear interpolation on
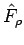 between the end points of the region
between the end points of the region
![$ \mathcal{R}= [x-h, x+h]$](img52.png) gives us an estimate for the slope
gives us an estimate for the slope
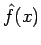 . [right] A non-linear regression on evaluations of 4 at all training samples, in this case on
. [right] A non-linear regression on evaluations of 4 at all training samples, in this case on
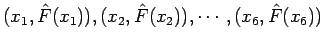 , yields a smooth estimate for the distribution function.
, yields a smooth estimate for the distribution function.
![\includegraphics[scale=1]{image_density_interpolation.eps}](img54.png) |
Figure 2:
Parametric Frequency Histogram Estimation: The true unknown density (top left) can be estimated by taking random samples (top right, 1000 random samples) and placing them in bins of fixed length to generate a histogram. Histograms with bin-size 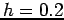 ,
, 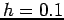 ,
, 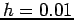 and
and 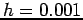 are shown; the bin-size or bandwidth (as well as the actual placement of the bins) is an important parameter in estimating the density function; in this case only a bin-size of
are shown; the bin-size or bandwidth (as well as the actual placement of the bins) is an important parameter in estimating the density function; in this case only a bin-size of 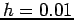 is able to capture the multi-modality of the true density. In the limit as the bandwidth goes to zero the histogram will converge to the true density provided the number of samples goes to infinity.
is able to capture the multi-modality of the true density. In the limit as the bandwidth goes to zero the histogram will converge to the true density provided the number of samples goes to infinity.
![\includegraphics[scale=0.5]{image_histogram_original_curve_01.eps}](img55.png)
![\includegraphics[scale=0.5]{image_histogram_random_samples_01.eps}](img56.png)
![\includegraphics[scale=0.5]{image_histogram_02_01.eps}](img57.png)
![\includegraphics[scale=0.5]{image_histogram_01_01.eps}](img58.png)
![\includegraphics[scale=0.5]{image_histogram_001_01.eps}](img59.png)
![\includegraphics[scale=0.5]{image_histogram_0001_01.eps}](img60.png) |
where
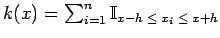 is the number of samples that fall in the region
is the number of samples that fall in the region
![$ \mathcal{R}= [x-h, x+h]$](img52.png) and
and 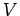 is the volume of
is the volume of
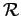 which in this case is simply
which in this case is simply 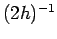 .
.
The shape of the region
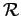 and hence its volume
and hence its volume 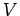 can be adjusted as more random samples become availible; it has been shown [DHS01] that as the regions
can be adjusted as more random samples become availible; it has been shown [DHS01] that as the regions
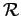 get smaller (
get smaller (
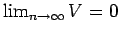 ) and the samples in the region increases (
) and the samples in the region increases (
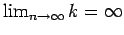 ), the estimated density
), the estimated density
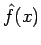 will converge to
will converge to 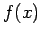 provided that
provided that
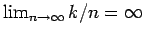 (that is to say the proportion of samples falling within the region to those outside it is very small); in the limit it will be a smooth density function.
(that is to say the proportion of samples falling within the region to those outside it is very small); in the limit it will be a smooth density function.


Next: Kernel Density Estimation: Parzen
Up: svkde
Previous: svkde
Rohan Shiloh SHAH
2006-12-12
![]() can be estimated from the data by taking the ratio of the number of samples that are less than or equal to
can be estimated from the data by taking the ratio of the number of samples that are less than or equal to ![]() to the total number of samples:
to the total number of samples:
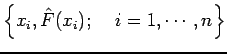
![]() we need to estimate the derivative of
we need to estimate the derivative of
![]() which can roughly be done by taking the difference between two evaluations of the distribution function at fixed lengths
which can roughly be done by taking the difference between two evaluations of the distribution function at fixed lengths ![]() and
and ![]() from
from ![]() :
:
![\includegraphics[scale=1]{image_density_interpolation.eps}](img54.png)
![\includegraphics[scale=0.5]{image_histogram_original_curve_01.eps}](img55.png)
![\includegraphics[scale=0.5]{image_histogram_random_samples_01.eps}](img56.png)
![\includegraphics[scale=0.5]{image_histogram_02_01.eps}](img57.png)
![\includegraphics[scale=0.5]{image_histogram_01_01.eps}](img58.png)
![\includegraphics[scale=0.5]{image_histogram_001_01.eps}](img59.png)
![\includegraphics[scale=0.5]{image_histogram_0001_01.eps}](img60.png)
![]() and hence its volume
and hence its volume ![]() can be adjusted as more random samples become availible; it has been shown [DHS01] that as the regions
can be adjusted as more random samples become availible; it has been shown [DHS01] that as the regions
![]() get smaller (
get smaller (
![]() ) and the samples in the region increases (
) and the samples in the region increases (
![]() ), the estimated density
), the estimated density
![]() will converge to
will converge to ![]() provided that
provided that
![]() (that is to say the proportion of samples falling within the region to those outside it is very small); in the limit it will be a smooth density function.
(that is to say the proportion of samples falling within the region to those outside it is very small); in the limit it will be a smooth density function.