APPROACH 1
<<---Previous Page NEXT Page >>
Prescriptive approach
Quick Menu:
FEATURE EXTRACTION: (#top)
The first step in this approach is to extract some intrinsic features from the music piece to be classified. The features considered by this approach can be classified into three categories: timbre related, rhythm related and pitch related.
Timbre is a property of any music piece. It is evaluated by considering the spectral distribution of the audio signal of the music piece (spectral refers to frequency). Timbre features are extracted for many small chunks of the piece, called frames. For every frame, a timbre value is computed. In order to compute a timbre value, many different methods have been used in the literature.
-FFT:
One of these methods relies on the classical FFT (Fast Fourier Transform) coefficients (an excellent tutorial on FFT is available at EPT's website (last visited on Nov. 3, 2005). In this case, for each frame, the feature vector would be the vector of the FFT coefficients.
-Cepstrum:
Another method people have used to calculate a timbre value are the Cepstrum Coefficients. This fancy name is not about a fancy concept. If you take the spectrum of the signal, take its log, and then take the inverse Fourier transform of that...you get the cepstrum:
![]()
Cepstrum coefficients are used because they make things easier. They reduce the dimension of the log-spectrum and smooth it, but keep the information carried by the spectrum.
-MFCC:
A related fancier term about a less fancy concept has also been used: the Mel Cepstrum Coefficients (MFCC). The Mel Cepstrum is the cepstrum computed after a non-linear warping onto perceptual frequency scale, the Mel-frequency scale.
Cepstrum and Mel Cepstrum have been used as feature for musical instrument recognition and also for speech recognition. A small digression: Many techniques that have been used in speech recognition have been tried as well in Music Genre Recognition. This means that there should be some structural analogy between text and music. Attempts to define this analogy have been numerous. The best analogy I have personally seen is presented in lecture 2 of Leonard Bernstein's talks at Harvard (Leonard Bernstein - The Unanswered Question [4]; available for rent at McGill music library or for sell at Amazon), where we have the following equivalence between music and language:
Note = Phoneme
Motive = Morpheme
Phrase = Word
Section = Clause
Movement = Sentence
Piece = Piece
According to this equivalence scheme, the entire movement of a symphony is surprisingly equivalent to only one sentence.
This analogy should be taken into account while trying to perform Music Genre Recognition using Speech recognition tools.
-Linear Prediction (LP):
LP is a way of encoding the spectral envelope of the audio signal, like MFCC. The Linear Prediction consists of a simple linear filter in which the source signal passes. The filter represents the effect of the resonating body of the musical instrument, its timbre. The coefficients of the linear filter (which are estimated in this process), control the position of the peaks on the power spectral density of the audio signal. For more information on LP and power spectral density you can consult the web-tutorial of Speech, Vision Robotics Group at Cambridge University (last visited on Nov. 3, 2005)
-MPEG filterbank components:
The above feature extraction methods are usually done on a raw .wav audio file, that is uncompressed data. However, most of the music we find today is compressed using the MPEG audio compression standard (MP3s are layer 3 MPEG compression). Hence, we either need to decompress the music into wav format before performing feature extraction, or we could calculate the features directly from the MPEG data.
-Spectral centroid:
It is simply the barycentre of the spectral distribution within a frame.
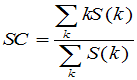
where S is the magnitude spectrum of a frame. The spectral centroid gives an indication of the shape of the spectrum, much like the center of mass could give an indication of the shape of a geometric figure.
-Spectral flux:
This measures the change in spectral shape from frame to frame.
![]()
where S[e] is the spectrum of frame e.
-Zero Crossing Rate (ZCR):
This measures, in the time domain, the zero-crossings that occur in a given frame (number of times the signal becomes zero during the time frame). It is an indication of the pitch and of the noise behavior of the signal. For further details regarding ZCR, and also regarding many of the feature extraction techniques we saw above, a very good lecture slideshow by Mark Hasegawa-Johnson at the University of Illinois at Urbana-Champaign can be accessed for consultation here (last visited on Nov. 3, 2005).
-Low order statistics:
Some people compute the low order statistics of the audio signal over a frame. They compute the first-order statistic, commonly known as the mean, the second-order statistic commonly referred to as variance, the 3rd-order statistic, also known as skewness, and finally they compute the 4th-order statistic, not commonly but known as kurtosis. An interesting fact: you can build the entire spectral distribution from the infinite series of its moments.
-Delta coefficients:
Delta coefficients are usually appended to the feature set in order to better take account of the dynamics of the data. As 'Delta' has always suggested to us, these coefficients are 'difference' coefficients, that is, they measure the change of coefficients between consecutive frames.
So much then for timbre related feature extraction. We have exposed the most commonly used techniques in this category. Readers are encouraged to consult the different reference links proposed throughout the exposition for further insight. Let us now move to rhythm related feature extraction.
Some authors do no limit feature extraction to timbre. They think that rhythm is an important descriptor to take into account too, and they are right because many music genres are mainly identified from the rhythm. A 3-beat Waltz could easily be confused with a steady 2-beat March if such a rhythmical transformation from 3-beats (Strong-weak-weak) to 2 beats (Strong-weak) were to be done. Well I've done this experiment to illustrate what I mean!
I took the first five phrases of Chopin's
Grande Valse Brillante, in E-flat major, op.18A,
and, after applying a quantization effect to transform the rhythm we get this
piece (apologies to Chopin...)
. If one does not know the melody and were to judge the genre of the piece solely
based on its rhythm, then chances are that he or she would not classify it as a Waltz
but rather as a kind of March, or something else.
In order to extract rhythm information, people resort to what they call 'beat histogram' built from the autocorrelation of the signal. Autocorrelation is simply a correlation between two values of the same variable at times Xi and Xi+k. It is the correlation between the audio signal and a time-shifted copy of the same signal. But usually, this technique is difficult to use to detect subtle rhythmical differences such as the ones seen among classical subgenres (as we just saw between waltz and march for example), rather, this technique is best for detecting radical rhythmic changes like the ones observed between a Rock piece and a Classical piece. To detect more subtle rhythms (and to preserve phase information), methods based on computing the entropy along with the autocorrelation have proven to be efficient [5] (You are recommended to consult the paper by D.Eck "Meter and Autocorrelation" for the mathematics and for some examples) .
According
to [2], and as far as my research was
concerned, only one explicit attempt at using pitch information for music genre
recognition is known. Pitch histograms feature vectors were used. Rock songs
typically have fewer peaks in the histogram than other genres, because they
rarely exhibit a high degree of harmonic variation. Jazz songs, on the other
hand, have denser histograms, as many different pitches are played at least once.
Remember, a pitch is nothing but a note (C, D, E, F, G, A, B
(or Do Ré Mi Fa Sol La Si in latin) and the chromatic notes in between
(sharp/flat)
)
CLASSIFICATION: (#top)
The next step is classification. Classification is based on supervised learning. In other words, some manually genre-labeled music pieces are used as training points. These training points will be used to classify unlabelled music pieces. This is the most commonly used method. However, the genre taxonomy used by the authors in the literature is always very simple and incomplete. There are very few classes (from 3 to 6). For example, some authors consider only 3 classes "Rock, Piano and Jazz". They label their training data using only these 3 labels, and try to classify a new unlabelled music piece into one of these 3 genres. Some authors also use 'garbage music', not because music in this category is garbage (though some music pieces deserve this title...), but as a category which takes into account every piece that is not in any of the other 3 to 6 genres.
Not only are the chosen taxonomies very
simple and incomplete (3 to 6 is a ridiculous range compared to the explosion of
genres that exists today), but they also carry many
ambiguities and inconsistencies.
The authors of [2] wonder, for
example, in "Rock, Piano and Jazz", where should a solo by Bill Evans
be classified. It is clearly both Piano and Jazz. Also, some people used
"Modern, Classical and Jazz" as their 3 classes. Again, isn't Jazz modern? What
is modern compared to Jazz then?
We already saw in the introduction and motivation sections how complex genres could be, so the work found in the literature based on this prescriptive approach seems highly controversial and maybe disappointing. In any case, we will take what has been done as a proof of concept rather than a solution to Music Genre Recognition. We will see in the second approach, the emergent approach, that things could become better, but still...
So after having chosen the class labels and manually labeled some training pieces, the authors proceed to the learning stage. Learning algorithms that have been explored for that purpose can be classified into three categories: Gaussian and Gaussian Mixture models, Linear or non-linear classifier, and finally Vector Quantization. (Note that Gaussian Mixture models are more often used in cases some data was unlabelled or in cases the manual labeling was not accurate and needed amelioration.)
-Gaussian and Gaussian Mixture models:
These models are used to explicitly estimate the probability density function of each genre class. The probability density is expressed as a weighted sum of simpler Gaussian densities (Gaussian Mixture).
-Linear or non-linear classifier:
Usually implemented by a feed-forward neural network. The first layer implements a non-linear function of the features (input to the network), usually using sigmoid neurons, that is, units which apply the function 1/e-w'x - w0 where x is the feature vector (computed from the techniques discussed above) and w is a weight vector that should be learned by the network. The second layer is a layer of perceptrons which are linear classifiers. The output of the network should be one of the genre-classes assumed a priori.
-Vector Quantization:
A set of reference vectors which can quantify the entire feature set with little distortion is sought during training. This set of reference vectors is like a codebook.
RESULTS: (#top)
Results of this approach are difficult to compare since each experiment done by the authors is different from the other in the taxonomy used, the training sets chosen, and implicitly, the definition of 'genre'. The results summarized in [2] are the following:
-Successful classification rates range between 48% and 90% across all experiments done by different authors. However, the 90% was achieved on a very small training and test set which may not be representative. Also the 48% was achieved using only pitch information. For the other results, the average number of songs used was 150.
Also, some authors studied genre specific results, that is, they evaluated the success rates for each genre considered in the training. On average, these authors got a rate of 95% for the 'Classical' genre, 85% for 'Jazz', 80% for 'Rock', 70% for 'Country'. Of course, these numbers might not be representative without providing the standard deviation of the results over several trainings. For more information, the reader can be referred to the papers referenced by [2].
Also, confusion matrices have been computed, and the result was that around 30% of 'Pop' songs were mistaken for 'Rock' by the learning algorithms. Very little confusion was reported between 'Classical' and 'Techno'. These confusion results are intuitively expected. 'Classical' is usually globally highly different from 'Techno'. Now in what ways they differ from each other is a different question that we will not address here, since the answer is highly subjective and philosophical (as we saw in the Introduction in the table that compares Elvis Presley and J-S. Bach). On the other hand, 'Pop' and 'Rock' have many similarities. Even humans tend to confuse Pop and Rock sometimes. Soltau (1998), quoted by [2], did an experiment on a group of 37 subjects exposed to the same training samples used in the learning algorithms. The subjects made the same confusions as the learning algorithms. This result proves again that there is no consensus on genre.
PROBLEMS: (#top)
There are many problems with this prescriptive approach. The 3 main ones are the following:
- Genre dependent features
Different genres have different set of features. For example, if you use as your feature vector the FFT coefficients, then, since Classical music has generally medium frequencies, using in the learning process a subset of coefficients that correspond to those frequencies yields much better prediction than using the entire coefficients set. 'Hip Hop' would use bass frequency. The confusion we saw between Pop and Rock comes in part from the fact that the frequency range of these two genres are very much overlapping, hence choosing only a feature vector that reflects timbre is not a good idea for classification in this case.
Hence, defining the best feature vector is data dependent, which obviously is a problem. Even if an optimal feature set is selected, adding new titles and new genres will modify it.
- Taxonomic Problems
Apart from the main taxonomic problem which is how to define a taxonomy, there are two problems to be considered: Hierarchical classification is needed, and growth is to be considered. By the first problem it is meant that classification should be based on genres first then sub-genres, then sub-sub-genres, and so on. So different levels of training should be made. This is needed because the error made by misclassifying 'East Coast Rap' as 'Southern Rap' is not as fatal or as important as the error made by misclassifying 'East Coast Rap' as 'Baroque' ! In other words, misclassification is tolerated if it occurs between sub-genres of the same genre, and it is more tolerated if it occurs between sub-sub genres of the same sub-genre, and so on.
This means that the learning algorithm should first classify into genres, then sub genres and so on, which is not easy to do with low-level features as this approach uses. This is easier to do with high-level features like "is there a guitar? a Piano?", "How many instruments are playing?", "Is the pianist using a lot the pedal? or not at all?" etc... Automatic High-level feature extraction is, unfortunately, still a dream...
The second problem is growth, and it is meant by this the evolution of genres both horizontally and vertically. Horizontally refers to new genres being created and vertically refers to new sub-genres added to an existing genre. This approach is not adaptive to evolution. Also, the number of genres that exist today (as seen in section 'Why? - Motivation') is huge. MSN Music Search Engine has more than 1000 genres. Finding a good and representative taxonomy is hence hard. Current results have difficulty classifying 'Rock' and 'Pop', so how would it discriminate finer subgenres?
- Classification with intrinsic attributes
This approach as we have seen is based on selecting intrinsic attributes as the feature-vector (timbre, pitch, rhythm). The use of these low-level features comes from a belief (supported by a study by Perrot and Gjerdigen (1999)) that only 250 milliseconds of audio are necessary for humans to accurately predict whether they like a music piece or not. This suggests that humans can judge a genre by using only immediate attributes (a combination of timbre, texture, rhythm, instrumentation...?) and without constructing higher level features (they don't have time to do that). However, this is contradictory with the fact we have seen in section 'What? - Introduction', which is that some genres are defined intentionally (extrinsically): Some genres are defined using high-level features, and even more, using cultural knowledge about the artist.
The authors of [2] did a quantitative study on 20000 music titles to show that genre definition cannot only be based on low level features such as timbre. They showed that many pairs of music pieces have radically different genres and yet the same timbre. For example:
-Schumann sonatas ('Classical') and Bill
Evans pieces ('Jazz'). Example: Piano sonata no.1 op.11
and Santa Claus is Coming to Town
-Prokofiev Symphony ('Classical') and an orchestral rendering of Gershwin's Porgy and Bess ('Jazz')
Similarly, they showed that many pairs of music pieces have radically different timbre and yet they belong to the same genre. For example:
-"Helter Skelter" and "Lucy in the Sky" by the Beatles
-"A Love Supreme" by John Coltrane and "My funny Valentine" sung by Chet Baker.
The study used MFCC to compute the timbre, since it has been shown to be the best among all other algorithms we saw above. The study computed timbral distances between a music piece and all other pieces and showed eventually that there is a poor correlation between genre and timbre.
All these problems of the prescriptive approach suggest that another (better?) approach should exist. Click on Next Page to go to the second approach, which is called the Emergent Approach.
<<---Previous Page NEXT Page >>
HOME WHAT ? WHY ? HOW? WHO ? Class 2005 Projects .Go to Top