Yes, it can be done very efficiently by linear programming (LP), and very importantly this can be done for very large scale problems, with practically no bounds on the size with an efficient LP solver.
The method is simple. The lifting technique we described in
3.2 immediately gives the idea. Recall that
the Voronoi diagram
of a set ![]() of
of ![]() points in
points in ![]() is the projection of the following
is the projection of the following ![]() -polyhedron to
-polyhedron to
![]() space of the first
space of the first ![]() components.
components.
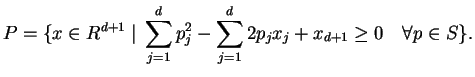
| (7) |
It is easy to see that two Voronoi cells ![]() and
and ![]() are adjacent if and only if the corresponding facets
are adjacent if and only if the corresponding facets ![]() and
and
![]() are adjacent in the polyhedron
are adjacent in the polyhedron ![]() .
Now, we formulate the following LP for any
distinct
.
Now, we formulate the following LP for any
distinct ![]() ,
,
![]() :
:
where ![]() is equal to
is equal to ![]() except for
except for ![]() th component
th component
![]() . The new inequality system
. The new inequality system
![]() is simply a modification of the original system
obtained by relaxing the
is simply a modification of the original system
obtained by relaxing the ![]() th inequality a little bit.
An important remark is, by definition (*),
th inequality a little bit.
An important remark is, by definition (*), ![]() and
and ![]() are adjacent if and only if the objective value
are adjacent if and only if the objective value ![]() is negative at an optimum solution. Thus we formulated
the Voronoi adjacency computation as an LP problem.
is negative at an optimum solution. Thus we formulated
the Voronoi adjacency computation as an LP problem.
How much do we gain by using LP for the adjacency computation, instead
of computing the whole Voronoi diagram?
A lot. It is hard to exaggerate this, because the LP (8)
(in fact any LP) is solvable in polynomial time,
whereas the associated Voronoi computation is exponential in
![]() and
and ![]() . Using the standard simplex method, the time complexity of solving
an LP is not polynomial, but the practical complexity is roughly
. Using the standard simplex method, the time complexity of solving
an LP is not polynomial, but the practical complexity is roughly
![]() .
.