


Next: How can one remove
Up: Convex Polyhedron
Previous: How hard is it
Contents
Is there an
efficient way of determining whether a given point 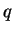 is in the convex hull of a given finite set
is in the convex hull of a given finite set 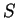 of points in
of points in 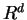 ?
?
Yes. However, we need to be careful.
First we give a method that we do not recommend but many people use.
This method computes an inequality
representation
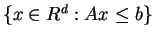 of
of 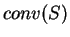 where
where
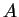 is some
is some
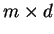 matrix and
matrix and 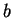 is a
is a 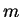 -vector.
This is called the convex hull computation
2.10. Once the system
-vector.
This is called the convex hull computation
2.10. Once the system 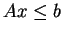 is
computed, it is easy to check whether
is
computed, it is easy to check whether 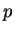 satisfies the system
or not.
satisfies the system
or not.
In most cases, this method is too expensive, since the convex
hull computation is very hard in general and impossible for
large data. In fact,
the number of inequalities in such a system 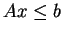 is often exponential in
is often exponential in 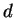 and
and 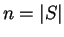 .
(This method might be of practical interests when we need to
remove lots of redundant points in clouds of points in small dimensions,
see 2.20.)
.
(This method might be of practical interests when we need to
remove lots of redundant points in clouds of points in small dimensions,
see 2.20.)
A standard method to check
whether 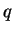 is in
is in 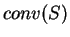 uses
linear programming (LP) technique 4.
An LP problem to be formulated for
the question is the following. Let
uses
linear programming (LP) technique 4.
An LP problem to be formulated for
the question is the following. Let
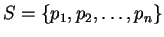 .
.
This problem has no objective function and such a problem is
often called a linear feasibility problem. Although it
might look simpler problem to solve, it is polynomially equivalent
to the general LP. In fact, it is usually a good idea to set up
an equivalent LP to solve it. More specifically, the problem
(3) has a solution if and only if the following
has no solution:
Geometrically, the meaning of this problem is simple. If it admits
a solution 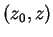 , then the set
, then the set
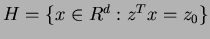 is a hyperplane in
is a hyperplane in 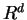 separating the polytope
separating the polytope 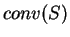 from the
inquiry point
from the
inquiry point 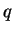 . Thus the existence of the separation means
the nonredundancy. Now, to actually solve the problem
(4), we set up the LP:
. Thus the existence of the separation means
the nonredundancy. Now, to actually solve the problem
(4), we set up the LP:
The last inequality is artificially added so that the LP has
a bounded solution. It is easy to see that the point 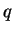 is
non-redundant if and only if the optimal value
is
non-redundant if and only if the optimal value 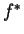 of
the LP (5) is (strictly) positive.
of
the LP (5) is (strictly) positive.



Next: How can one remove
Up: Convex Polyhedron
Previous: How hard is it
Contents
Komei Fukuda
2004-08-26
![]() of
of ![]() where
where
![]() is some
is some
![]() matrix and
matrix and ![]() is a
is a ![]() -vector.
This is called the convex hull computation
2.10. Once the system
-vector.
This is called the convex hull computation
2.10. Once the system ![]() is
computed, it is easy to check whether
is
computed, it is easy to check whether ![]() satisfies the system
or not.
satisfies the system
or not.
![]() is often exponential in
is often exponential in ![]() and
and ![]() .
(This method might be of practical interests when we need to
remove lots of redundant points in clouds of points in small dimensions,
see 2.20.)
.
(This method might be of practical interests when we need to
remove lots of redundant points in clouds of points in small dimensions,
see 2.20.)
![]() is in
is in ![]() uses
linear programming (LP) technique 4.
An LP problem to be formulated for
the question is the following. Let
uses
linear programming (LP) technique 4.
An LP problem to be formulated for
the question is the following. Let
![]() .
.