Lesson 23 - Learning Goals

• Want to find a root or zero of f(x) on an interval [a,b], i.e. a < xroot < b such that f(xroot) = 0.

• Although the formula for f(x) is known, algebraic techniques for solving f(x)=0 may not work (e.g. arbitrary quintic or polynomial of degree 5; transcendental functions such as f(x) = tan x - e^x).

• A number of iterative techniques allow us to obtain successively better approximations of the root, xroot.
  
  

BISECTION (INTERNAL HALVING)

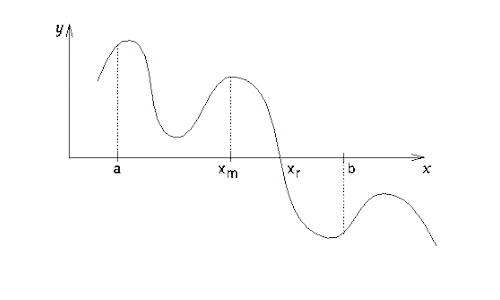
Start with an interval [a,b] containing a single root.

This means the arithmetic signs of f(a) and f(b) will be different (one positive, one negative).

General idea: Compute the interval midpoint x_m, which then replaces the interval limit with matching sign. Repeat, stopping when f(x_m) is "small", or when the interval becomes "small" (less than a small positive constant ).

Note that the size of the interval is halved at each step.

BISECTION - ALGORITHM

• xlow=a , xhigh=b
  
• xmiddle = (xlow + xhigh) /2
  
• if |f(xmiddle)| < 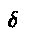or |xlow - xhigh| < 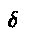then xroot = xmiddle, STOP.
  
• if f(xmiddle) * f(xhigh) < 0 then xlow = xmiddle , else xhigh = xmiddle
  
• go to step 2
  
  
  
  
  

NEWTON-RAPHSON METHOD

• Have a guess, x_i ,at the root.
  
  
• An improved guess, x_i+1, is a point at which the line tangent to the curve at (x_i, f(x_i)) intersects the x axis.
  
  
• Repeat iteration, stopping when |f(x_i+1)| < 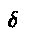, or |x_i+1 - x_i| < 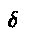, concluding that xroot = x_i+1 .
  
  
  

DERIVATION OF x_i+1

• Equation of line tangent to curve y=f(x) at the point (x_i , y_i) is
  
• y-y_i= m*(x-x_i)
  
• The slope, m, is given by the value of the derivative of y, evaluated at the point (x_i , y_i)
  
• m=f '(x_i)
  
• Also know that point (x_i+1, 0) is on the line:
  
• 0 - y_i = f '(x_i) * (x_i+1 - x_i)
  
• x_i+1 = x_i - f(x_i)/f '(x_i)
  
  

Disadvantages:

• Must compute the derivative f '(x), which may be hard, costly.
• Possible oscillatory behaviour (e.g. f(x)=sin x)
  
  

SECANT METHOD

• Start with two guesses at the root: x_i and x_i+1, with |f(x_i+1)| < |f(x_i)|
  
  
• Approximate the tangent to the curve at (x_i, f(x_i)) by the secant.
  
  
• The secant is the line through (x_i , f(x_i)) and (x_i+1, f(x_i+1)).
  
  
• An improved guess, x_i+2 , is the point at which the secant line intersects the x-axis.
  
  
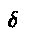• Repeat iteration, stopping when |f(x_i+2)| < , or |x_i+2 - x_i+1| < 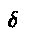, concluding that xroot = x_i+2 .
  
  

/* Implementation of the secant method */

#include <math.h>
#define TRUE 1
#define FALSE 0

double secant(
   double (*f)(double), /* function to find root of */
   double x1, /* start of interval */
   double x2, /* end of interval */
   double epsilon, /* tolerance */
   int max_tries, /* maximum # of tries */
   int *found_flag) /* pointer to flag indicating
                      success */

{
   int count = 0; /* counter of loops */
   double root = x1; /* root value */
   *found_flag = TRUE; /* initialize flag to success */

   while( fabs(x2-x1)>epsilon) /*check for convergence */
   {
      root = x1 - f(x1)*(x2-x1)/(f(x2)-f(x1));
      x1 = x2;
      x2 = root;
      count = count + 1;
   }
   if( fabs(x2-x1) > epsilon ) /*check for convergence */
      *found_flag = FALSE;

   return(root); /* return root */
}