NUMERICAL INTEGRATION
This chapter is the first of the series that addresses some of the numerical
techniques used. Numerical integration is very useful in situations where an
exact solution to an integration problem cannot be found analytically.
The techniques described are the Midpoint, Trapezoidal and Simpson's rules. A
comparison shows that Simpson's Rule is clearly superior to the others.
Associated with this chapter is also a graphical demonstration of the different
methods. This is available on the associated diskette and is also accessible
over the Internet.
INTRODUCTION
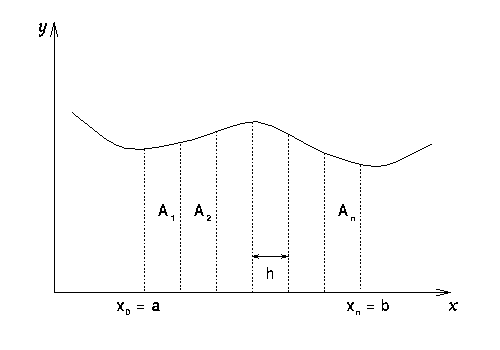
- Given a function y=f(x)
- Want area under curve between x=a and x=b
- Assume we cannot obtain an exact solution, or perhaps f(x) is unknown, and we only have data points (xi,yi).
- Main idea: Break area under curve into n panels
of width h: A = Ai , h = (b-a)/n
- How to calculate Ai ?
- Many methods of approximation
- All estimates improve with larger n, as h
 0 .
0 .
MIDPOINT RULE
- Use rectangular panels (i.e. assume f(x) is constant and equal to y* between xi-1 and xi )
- Three possibilities:
- Left endpoint: y* = yi-1 = f(xi-1)
- Right endpoint: y* = yi = f(xi) = f(xi-1 + h)
- Midpoint: y* = yi - ½ = f( (xi-1 + xi)/2 ) = f(xi-1 + h/2)
- On average, midpoint looks like best guess
MIDPOINT RULE ALGORITHM
We wish to integrate y=f(x) from x=a to
x=b using n rectangular panels of equal width.
h = (b-a) /n
x0 = a
xi = xi-1 + h
Ai = h* f( (xi-1 + xi)/2 )
A 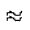
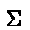 Ai (i=1
Ai (i=1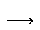 i=n)
i=n)
A 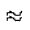 h* [
h* [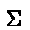 f( (xi-1 + xi) /2 )] (i=1
f( (xi-1 + xi) /2 )] (i=1 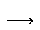 i=n)
i=n)
REAL FUNCTION MidPt(x0, x1, N)
! Estimate the area under F between x0 and x1
! using the Midpoint Rule with N panels.
REAL x0, x1, x, h, Sum
INTEGER N
h = (x1 - x0) / N
Sum = 0.0
! Add area of each panel, assuming unit width
! and multiplying by the true width h later.
x = x0+h/2.0 ! Initial start is middle of first panel
L1: DO k= 1,N
Sum = Sum + F(x)
x = x + h
END DO L1
MidPt = h*Sum
RETURN
C Version
double midpoint(double x0, double x1, int n)
{
double h, sum;
/* Calculate panel width h; initialize Sum. */
h= (x1 - x0) / n;
x0= x0 + h/2;
sum= 0;
/* Add area of each panel, multiplying
by the true width h only once later. */
do {
sum= sum + f(x0);
x0= x0 + h;
}while(x0 x1);
return(sum * h);
}
TRAPEZOIDAL RULE
Try taking average of the expressions for rectangular
Ai, with f evaluated at left and right endpoints
Ai = [ h f(xi-1) + h f(xi) ]/2
Ai = h/2 [ f(xi-1) + f(xi) ]
Approximate Ai, as the area of trapezoid abcd.
Trapezoidal method appears to take 2 function evaluations per
panel, but
Ai + Ai+1= h/2 [ f(xi-1) + f(xi) ] + h/2 [ f(xi)
+ f(xi+1) ]
Ai + Ai+1 = h/2 [ f(xi-1) + 2f(xi) + f(xi+1) ]
For n panels, need only n+1 evaluations of f.
TRAPEZOIDAL RULE ALGORITHM
We wish to integrate y=f(x) from x=a to x=b using
n trapezoidal panels of equal width.
h= (b-a)/n
x0 = a
xn = b
xi = xi-1 + h
Ai = h/2 [ f(xi-1) + f(xi) ]
A 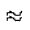
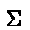 Ai (i=1
Ai (i=1  i=n)
i=n)
A 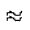 h [ ( f(x0) + f(xn) ) / 2
+
h [ ( f(x0) + f(xn) ) / 2
+ 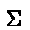 f(xi) ] (summing from i = 1 to n-1 )
f(xi) ] (summing from i = 1 to n-1 )
SIMPSON'S RULE
In Trapezoidal rule, successive points (xi, yi) were joined with straight lines
Now, fit a parabola to 3 points (xi-2, yi-2), (xi-1, yi-1), and (xi, yi) for better accuracy
One panel (width 2h) now includes 3 points
h = (b-a)/n
b-a = nh
n must therefore be even
From geometry or Taylor series expansion, we find
Ai = h/3 [ f(xi-2) + 4f(xi-1) + f(xi) ] , for i = 2,4,6,…,n
Once more, combine expressions for adjacent panels and simplify.
Ai + Ai+2 = h/3 [ f(xi-2) + 4f(xi-1) + 2f(xi) + 4f(xi+1)
+ f(xi+2) ]
For n panels, again need only n+1 evaluations of
f.
SIMPSON'S RULE ALGORITHM
We wish to integrate y=f(x) from x=a to x=b using
n/2 double parabolic panels of equal width.
h = (b-a)/n
x0= a
xn= b
xi= xi-1 + h
Ai = h/3 [ f(xi-2) + 4f(xi-1) + f(xi) ]
A 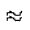
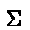 Ai (i=1
Ai (i=1  i=n)
i=n)
A 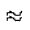 h/3 [ f(x0) + f(xn) + 4
h/3 [ f(x0) + f(xn) + 4 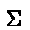 f(xi) + 2
f(xi) + 2 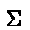 f(xi) ]
f(xi) ]
where first 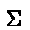 is from i=1 to n-1
is from i=1 to n-1
and second 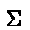 is from i=2 to n-2
is from i=2 to n-2
ADAPTIVE INTEGRATION PROCEDURE
- Arbitrary precision
ADVANCED, RECURSIVE ADAPTIVE INTEGRATION TECHNIQUE
/* more sophisticated adaptive integration method
using recursion */
On to the next lecture
Go back to lecture menu
 Browse other websites on this topic
Browse other websites on this topic