COMP-360 Assignment #5 Solutions

Questions 1 - 4 are out of 10 and question 5 is out of 40, for a total of 80 marks overall. For questions about the assignment or about the marking scheme, please contact Theresa at theresa (dot) deering (at) mail.mcgill.ca (questions 1 and 2) or Gheorghe (questions 3 and 4) at ghitzah (at) gmail (dot) com or both (question 5). View the questions here.

1. • a:

     We first show that VERTEX COVER is in NP. The certificate is a set S of vertices. A polynomial time certifier is to check that each edge has at least one endpoint in S and check that |S| = k.

   • b:

     To reduce from SAT to VERTEX COVER, we assume that we have a black box VERTEX COVER-solver that we can use a polynomial number of times in order to solve SAT.

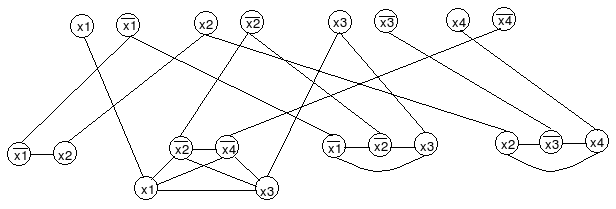
     In SAT, we are given a set X of n Boolean variables x1, ..., xn and a set C of m clauses c1, ..., cm where a variable can be either TRUE or FALSE, a term is either a variable xi or its negation, and a clause is a disjunction of some number of terms t1, ..., tl. SAT should say YES if there is an assignment of the variables such that all the clauses in C evaluate to TRUE.

     To convert this to an instance of VERTEX COVER, we need to map these values to elements of a graph, G.
     Add a node for each term an dadd an edge between pairs with the same variable. Note that at least one of these nodes will be in S in order to cover this node. Call these truth-pairs.
     For each clause, create a complete graph with the terms as new vertices. Note that to cover all these edges, at least (sizeOfClause - 1) of the nodes must be in S
     For each term in the truth-pairs, add an edge between it and all matching terms in the clauses.
     Let the size of S be |V| - n - m

     Proof:
     If there is a vertex cover of size |V| - n - m then the terms corresponding to the ones in S have the property that if they are TRUE then every clause is satisfied.
     If every clause is satisfied then choosing the TRUE terms to be in S will allow us to find a vertex cover of size |V| - n - m.

   • c:

     

2. For solution, see here.

3. For solution, see here.

4. First, we need to show that the problem SHIP is in NP. The certificate is the set of items to send. The polynomial time certifier is to check that the total value of the items is greater than or equal to C, the total weight of the items is less than or equal to W, and the total volume of the items is less than or equal to V.

   Second, we choose a known-NP complete problem to reduce from. We will reduce SUBSET SUM to SHIP.

   Third, we morph the general SUBSET SUM problem into an instance of the SHIP problem. Note the definition of SUBSET SUM: Given a set of natural numbers a1, ..., an, is there a subset such that the elements sum to exactly the integer A?
   Set ci = ai for i = 1, ..., n
   Set wi = ai for i = 1, ..., n
   Set vi = ai for i = 1, ..., n
   Set C = A
   Set W = A
   Set V = A

   Last, we prove that it works:
   If we have a subset that sums exactly to A then we have a set of items to ship that has a cost summing exactly to C, a weight summing exactly to W, and a volume summing exactly to V. This is a set that it is worth it to ship.
   If we have a set that is worth it to ship, then we have its cost summing to at least C = A and its weight summing to at most W = A. Since all the cis equal all the wis, we know that total is both at least A and at most A. Thus, the totals C, W, and V all equal A. This gives us a set of objects that sum exactly to A, our SUBSET SUM.