A number of people had problems with the definition of a cut. The
size of a cut is determined by the CAPACITY of the edges from A
to B, not the flow.
Also keep in mind that the Ford-Fulkerson algorithm adds only one simple
s-t path per iteration of the algorithm. You cannot add more than one
path at a time and it still be the algorithm described in the textbook.
- a:
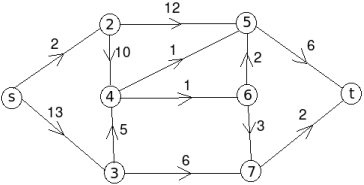
- b:
Let the edge-labels on the graphs G represent capacity(flow).
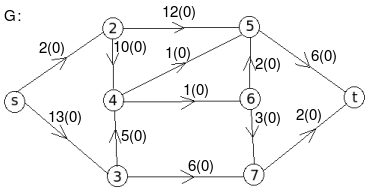
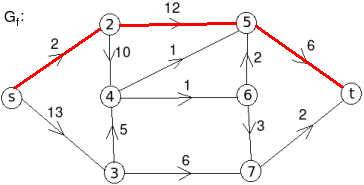
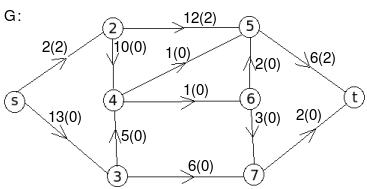
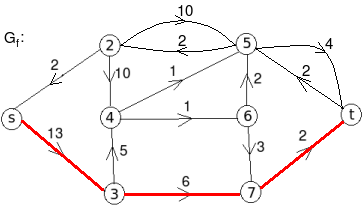
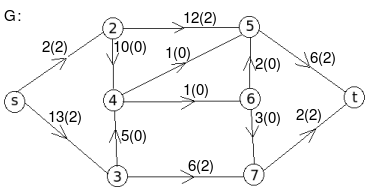
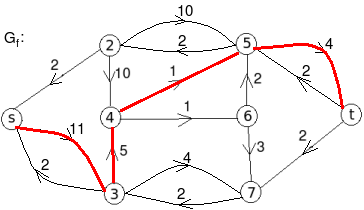
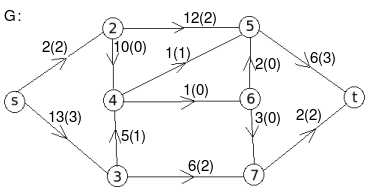
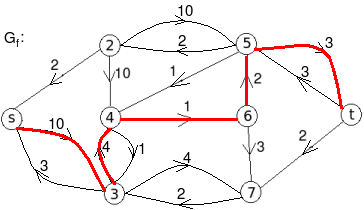
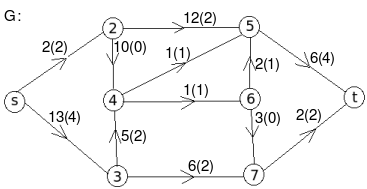
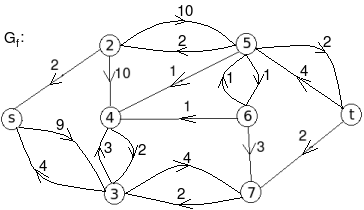
- c:
The minimum cut is highlighted in green.
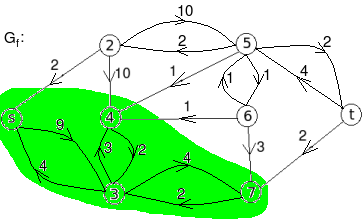
Therefore, the minimum cut has capacity 6 and the maximum flow has flow 6.
The main problem with this question was distinguishing between FLOW and CAPACITY. Most people used the idea of the fraction 1/k and then tried to use the Integrality Theorem, but they said that the 1/k was the capacity. There are 2 problems with this statement: If the edge capacity is a fraction then the integrality theorem no longer holds (must have integer capacities to guarantee an integer flow), and the max flow given by the Ford-Fulkerson algorithm will be 0 (the Ford Fulkerson only produces integer solutions and no integer flow other than 0 can flow over an edge of capactiy 1/k).
- a:
I: Constructing the network flow:
Beginning with a compatibility graph G, as described in the question. Let each of the n interns be a vertex in a set N. Let each of the m hospitals be a vertex in a set M. Note that N and M are disjoint.
Construct a network flow, G', as follows:
- Add a node s.
- Add a directed edge (s, x) for each x in N, and assign each of those edges capacity 1.
- Direct each edge (x, y) in the edge set of G from the vertex x in N to the vertex y in M, and assign each of those edges capacity 1.
- Add a node t.
- Add a directed edge (i, t) for each i in M, and assign each of these edges capacity d(i).
II: Proving that it is always possible to assign each intern to a compatible hospital:
First, look at the s,t cut formed by the set A = {s} and B = G' \ {s}. By construction, there are n edges from A to B and each of those edges has capacity 1. So, there exists a cut with capacity n.
Second, let's add some flow to each of the edges. Let each edge coming out of s have a flow of 1. Let each edge from N to M have flow 1/k. Let each edge from M to t have a flow of d(i). This preserves the capacity conditions because each edge's flow is no less than 0 and no greater than the edge's capacity. This preserves the conservation conditions because
- s has no inflow because it is the source and has outflow of 1 on each of its n outgoing edges for a total outflow of n.
- Each vertex x in N has inflow of 1 from s and outflow of 1/k on each of its k edges for a total outflow of 1. Therefore, inflow(x) = outflow(x).
- Each vertex i in M has inflow of 1/k from each of its k * d(i) incoming edges for a total inflow of d(i) and outflow of d(i). Therefore, inflow(i) = outflow(i).
- t has inflow d(i) from each of its m incoming edges for a total inflow of n (because if we count the edges going out of N there are k * n edges, and if we count the number of edges going into M there are k * the sum of all d(i) edges. This is just counting the same edges in two different ways. So k * n = k * sum of all d(i). Thus, cancelling out the k, we get n = the sum of all d(i)) and has no outflow because it is the sink.
This flow has value n (since that is the amount of flow generated by the source).
Since there exists a cut of size n and a flow of value n, n is the maximum flow (by the max-flow min-cut theorem).
By the integrality theorem, there exists a flow of value n for which the flow along each edge is an integer. This integral flow can be found using, for example, the Ford-Fulkerson algorithm, and it always provides us with an assignment of each intern to a compatible hospital.
- b:
One possible compatibility graph G:
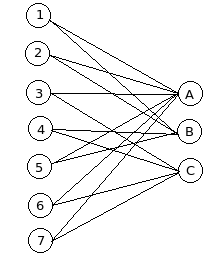
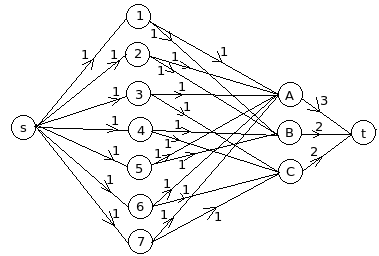
The corresponding network graph G' (the edge labels are capacities):
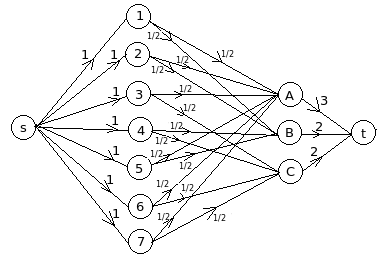
Illustrating the max flow using fractional flow values (the edge labels are flows):
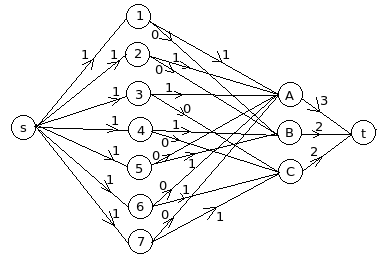
Illustrating one possible integer max flow (the edge labels are flows):
This question seemed well-understood. Some people forgot to specify how many paths they needed to binary search or how they got the paths or how they knew that there were going to be exactly k paths in the max flow after the Ford-Fulkerson algorithm.
For solution, see here.
Most people did not understand the definition of test set. The pairs
in the test set can, and in some cases must, have repeated laptops and
access points. The definition of test set only talks about the RANGE
not whether or not the laptops are actually connected to a particular
access point. This caused problems in both part a and part b.
A lot of people associated max flow directly with whether or not there
could be a test set of size k. This only works in the special
case when the max flow is n (i.e. a perfect matching).
For solution, see here.