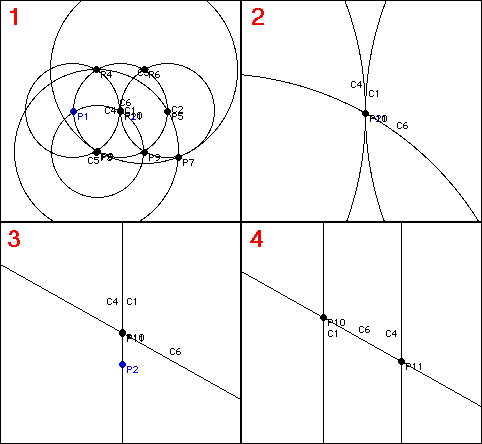
Starting with two points P1 and P2 that are 1 unit apart, the following construction (which makes use of only 6 circles) places P10 and P11 1.436x10-7 unit apart!
C1 = circle(P1,P2) C2 = circle(P2,P1) P3 = intersect(C2,C1) P4 = intersect(C1,C2) C3 = circle(P3,P4) P5 = intersect(C2,C3) C4 = circle(P5,P2) P6 = intersect(C2,C4) P7 = intersect(C4,C3) C5 = circle(P6,P7) P8 = intersect(C5,C1) // zoom P3 for this one P9 = intersect(C4,C2) C6 = circle(P8,P9) P10 = intersect(C1,C6) // not quite P2! zoom a lot to see the intersection P11 = intersect(C6,C4) // zoom a lot more to differentiate from P10!
Here's a succession of zooms, with P10 & P11 at the center of each image.
