Vector Calculations

Hofmann-Engl [5] describes several possible calculations for melodic similarity based upon his idea of melodic chains. He defines the similarity of two melodies to be a function of what he calls the interval vector and the similarity vector. The similarity vector is defined to be the vector difference between the individual pitch values of the melodic vectors M₁ and M₂:

$\displaystyle V_S = [m_{21}-m_{11}, m_{22}-m_{12}, \dots m_{2n}-m_{1n}]$

The interval vector is defined to consist of the differences between adjacent members of the similarity vector:

$\displaystyle V_I = [s_2 - s_1, s_3 - s_2, \dots s_n - s_{n-1}]$

Recall that because these pitch values are logarithms, so that these differences can be thought of as the ratios of the fundamental frequencies of the notes in each melodic chain.

The similarity S between two pitch vectors is then defined in terms of the product of two values, one derived from the similarity vector and the other derived from the interval vector. In other words:

S = F₁(V_S) F₂(V_I)

The S value will be in the range zero to one, where one is perfect agreement. The subfunctions are then defined as follows:

$\displaystyle F_1(V_S) = \sqrt{\frac{\sum_{i=1}^{n}\left(e^{-\frac{k_1}{n}s_i^2}\right)}{n}}$

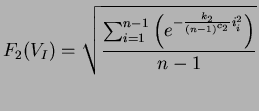
$\displaystyle F_2(V_I) = \sqrt{\frac{\sum_{i=1}^{n-1}\left(e^{-\frac{k_2}{n-1}i_i^2}\right)}{n-1}}$

In these equations c₁, c₂, k₁ and k₂ are constants, and s_i and i_i are the ith element of the similarity and interval vectors.

In his own experiments, Hofmann-Engl adjusts the values of the constants to match results from experiments with human subjects.