Lesson 25 - Learning Goals

THE EULER METHOD

• Given y'= f(x,y)

• Approximate y' at point (x_i , y_i) by the slope of the line joining it and (x_i+1 , y_i+1);
        y'(x_i , y_i)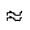 (y_i+1 - y_i) / (x_i+1 - x_i) = (y_i+1 - y_i) / h

• Then conclude f(x_i , y_i) 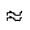(y_i+1 - y_i) / h ,
         and y_i+1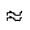 y_i + h f(x_i , y_i)
  

• Analysis shows error in estimate h (very inaccurate 1st order method)

• Stability of the approximate solution is questionable - whether error in estimation introduces an additional parasitic solution to the differential equation that overwhelms the true solution.

• Roundoff error is also a problem.
  
  
  

EULER ALGORITHM

Starting from the point (0 , y₀), we estimate the solution to y' = f(x,y) at x-values separated by the step size h, until we reach the desired value x_f of x. It is assumed that x_f = n h for some positive integer n, which is the number of steps taken in attaining the final solution.

1. x = 0 , y = y₀
2. if(x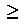x_f) , STOP
3. y = y + h* f(x,y)
4. x = x + h
5. go to step 2

THE RUNGE-KUTTA METHOD

• This is a whole class of formulae of which one interests us.
• The fourth order method has error 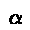h4, making it very much better than the Euler method.

Advantages
(relative to more complicated techniques):

• Easy to program
• Good stability
• Easy to change step size
• Self starting (only one initial point is required)
• Reasonably accurate
  
  

The derivation of the formula is too complex, but basic idea is to start from (x_i , y_i) and use Euler method to obtain different estimates of y_{i + ½} and y_i+1 which are combined so as to minimize error:

y*_{i + ½} = y_i + h/2 f(x_i , y_i)

y**_{i + ½} = y_i + h/2 f(x_{i + ½} , y*_{i + ½})

y*_{i + 1} = y_i + h f(x_{i + ½} , y**_{i + ½})

y_{i + 1} = y_i + h/6 [ f(x_i , y_i) + 2f(x_{i + ½} , y*_{i + ½})

+2f(x_{i + ½} , y**_{i + ½}) + f(x_{i + 1} , y*_{i + 1)} ]

To use the Runge-Kutta method, start with y(0) = y₀, and apply the above equations (in sequence!) to get y₁ = y(h).

Repeat this process for x₂, … , x_n where x_n = nh.