Lesson 21 - Learning Goals

• e.g. n integers to be sorted in increasing order from smallest to largest:

• Want algorithms (methods, paradigms, …) to do this efficiently - compact and fast.

• Compact : little extra space needed

• Speed : running time of the algorithm [ Best Case? Worst Case? Average Case? ]

ORDER NOTATION

• Allows description of the "running time" of the algorithm as a function of the size, n, of the input

• Algorithm is O(f(n)) if running time is bounded by c f(n) (where c is a positive constant) for all inputs of size n.

• Note: For large n, 0.001 n³ >> 10⁶ n² , so c "doesn't matter".

• e.g: A sorting algorithm technique is O(n²) if its "running time" is proportional to n² for input arrays of length n.

• Algorithm is 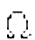(g(n)) if running time is greater than d g(n) (where d is a positive constant) for some input of size n. O provides an upper bound on running time, while 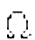provides a lower bound.

FOR SORTING:

• Running time can measure the number of swaps (exchanges of array elements) or the number of comparisons.

• Theoretical result: sorting problem is (n log n) (i.e. cannot do better)

• Practical result: There exist algorithms that work in O(n log n) time

• For small n, (e.g. n<100), some simple O(n²) algorithms are faster than the elegant O(n log n) ones.
  

BUBBLE SORT

• Imagine a vertical array, where smaller elements are "lighter" and bubble up to the top during sorting.

• Make repeated, bottom-to-top passes, exchanging adjacent elements as we go.

• On the first pass, the lightest element bubbles up to the top, etc.

      A(1) small

      A(2) .

      A(3) .

      … .

      A(n) big

BUBBLE SORT ALGORITHM

       for i = 1 to n do

       for j = n down to i + 1 do

       if A[j] < A[j-1] then

       Swap(A[j] , A[j-1])

• Note that, after i passes, the array elements A[1], A[2], … A[i] are in their final, sorted order.

• Need a total of n-1 passes, because if n-1 smallest elements are sorted, then so is the nth, largest one.

• This process requires O(n²) swaps, O(n²) comparisons, and only 1 extra record in the swap procedure.
  
  

INSERTION SORT

• On pass i, the array element A[i] assumes its rightful position among the A[1], A[2], …, A[i-1], which were already sorted on previous passes.

• Basic Idea : For each I from 2 to n, move A[i] to position j <= i such that A[i] < A[k] for j k < i, and either A[i] A[j-1] or j = 1.

• Convenient to set A[0] = - to avoid checking j=1.
  
  

ALGORITHM FOR INSERTION SORT

        A[0] = -MaxInt

        for i = 2 to n do begin

        j = i

        while A[j] < A[j-1] do begin

        Swap(A[j], A[j-1])

        j = j - 1

        end

        end

• Note that the partial results are not useful (element A[i] may take any place amongst the elements A[1], A[2], …, A[i1] on pass i)

• Again requires O(n²) swaps, O(n²) comparisons, little extra space.
  

SELECTION SORT

• On pass I, select the smallest array element A[j] amongst A[i], A[i + 1], …, A[n]
  
• Then, swap A[i] and A[j]
  
• This leaves elements A[1], A[2], …,A[i] in their final, sorted order.
  
• Running time is still O(n²), but there are only n-1 swaps; may be useful if records are large and swaps are "expensive"
  
  

ALGORITHM FOR SELECTION SORT

        for i = 1 to n - 1 do begin

        j = i

        Min = A[i]

        for k = i + 1 to n do

        if A[k] < Min then begin

        Min = A[k]

        j = k

        end

        end

        Swap( A[i], A[j])

        end

SHELL SORT

• On pass 1 sort n/2 pairs of elements (A[i], A[n/2 + i]), for 1 i n/2

• On pass 2 sort n/4 4-tuples of elements (A[I], A[n/4 + i], A[n/2 + i], A[3n/4 + i]), for 1 i n/4

• On pass j, sort n/2j 2j-tuples of elements (A[i + kn/2j]), 0 k 2j - 1, for 1 i n/2j

• Stop when j > log2n

• Use insertion sort on the tuples in each pass, stopping once 2 elements in the proper order are encountered

• Analysis shows O(n^1.5) running time
  

BETTER ALGROITHMS

• Shell sort is reasonably fast and easy to implement

• Quicksort is O(n log n) in average case, but O(n²) in worst

• Heapsort is O(n log n) in average and worst case, but the constant is big, so worse algorithms better for "small" problems.