So how does learning work?

I've asked a lot of people how learning works and nearly every time the response is synaptic plasticity. It refers to the curious process by which synapses - connections between neurons - strengthen or weaken in response to co-occurring activity in neurons, and I probably hear about it more often than anything else in the neuroscience universe.

Still, it's a bit odd, equivalent to asking a computer scientist how computer programs work and receiving an answer instead about how a transistor switches state. So how does learning actually work? Either the neuroscience community hasn't figured it out yet, or they're delighting in leaving us on a cliffhanger.

I went and tried to uncover what we know and don't know about how learning actually works. I also took a deep dive into some selected works with ideas that I found particularly interesting and share them here in as plain of English as possible.

Broadly, there seems to be three interesting approaches. One: you could measure things in the brain directly. This is a hard thing to do in the case of anything that involves organic material, and in particular establishing a causal link between synaptic activity and behavioural output would require a large number of simultaneous recordings in vivo (Humeau and Choquet, 2019). Short of a perfect experiment like that, we could ask other questions about the brain's physical structures, hoping to infer processes from substrate.

Two: you could take what you already know about the substrate and design learning algorithms that match biological constraints. You run simulations on your models, test how well they learn empirically, and iterate on the design of your models using their performance as your guiding light.

Three: you can create models that work empirically and theorize about their similarity to biological learning. This seems a bit ridiculous, but given that we've managed to create our own working learning algorithms in the past few years by way of ANNs, we can ask questions about whether there are similar mechanisms in the brain. In one direction you have neuroscience informing the design of better AI, in another you have novel, performative ANN designs, which may inspire theories about neuroscience.

Not to say that these approaches are mutually exclusive—in fact, they are required to inform each other. But I think it's a good layout for our exploration.

Background

First, a little bit of definition. Learning is when the brain takes in new information—from any sensory modality—and either stores it or represents it in a way that modulates future activities. It includes a broad range of tasks like motor training, object recognition, and explicit memory formation. Clearly, this is happening all the time in humans and is arguably the substance of intelligence.

To understand learning is to figure out what's happening at the synaptic, cellular, and network levels during learning.

Synaptic plasticity

Synaptic plasticity can be thought of as the atomic subunit of learning. We discovered this fairly early on, as scientists in the late 1800s found that an adult and a baby have roughly the same number of neurons. In other words, new knowledge could not be the result of new neuron production, and information must instead be contained in the connections between neurons. The 1950s were when Donald Hebb proposed how this might arise—coincident activity in the pre- and postsynaptic neurons would strengthen the synapse, making the postsynaptic neuron more sensitive to future activity (Hebb, 1949).

Long-term synaptic plasticity was discovered in the 1970s (Bliss and Lomo, 1973). It involves metabolic and structural changes to the synapse that increase (long-term potentiation, LTP) or decrease (long-term depression, LTD) the efficacy of signal transmission.

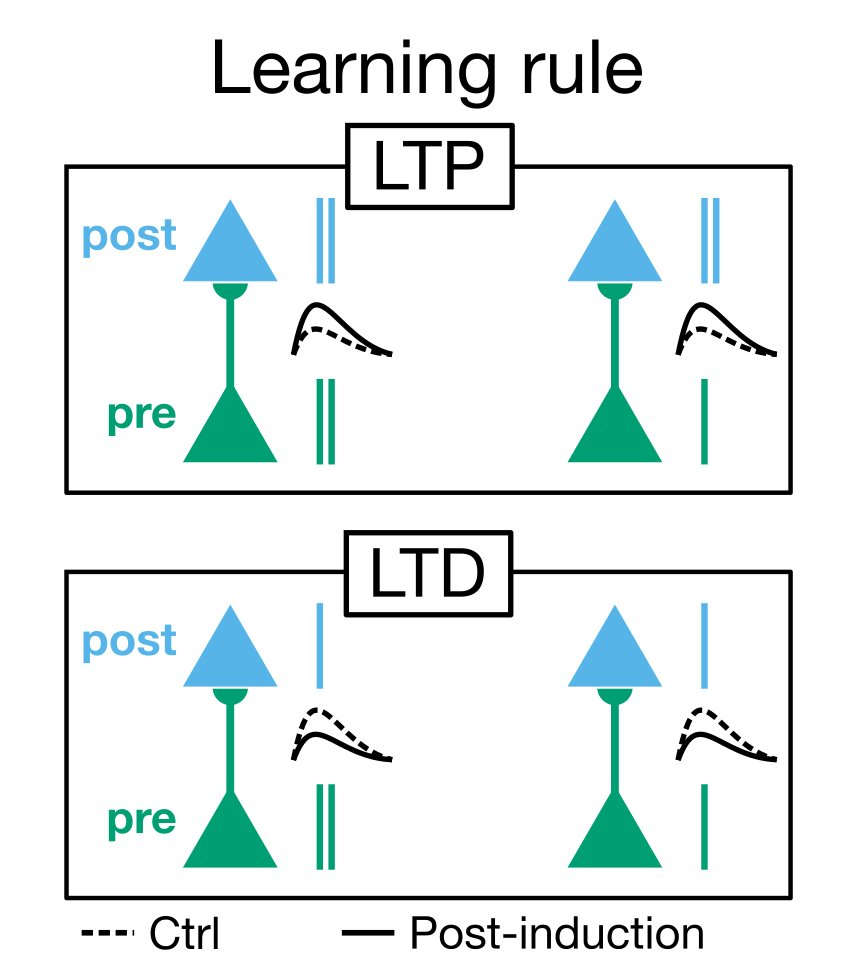
The canonical evidence for LTP and LTD comes from fear conditioning experiments where a cue is associated with a foot shock. The experiment is conceptually very straightforward: you have two coincident stimuli, and "learning" consists of associating one stimulus (the cue) with the other (the foot shock) upon further exposure to the first. After chemically blocking LTP, the animal no longer learns the association and does not respond to the cue.

LTP is highly illuminating for local circuits and simple processes involving few synapses. But what about explicit memories? Memories are known to be encoded in multiple neurons in complex and not entirely well-understood distributions across the cortex. Further, what about complex tasks involving hierarchical networks? It is hypothesized that brain networks are structured in a hierarchy from low-level receptors to high-level neurons in the cortex. How do you propagate LTP or LTD from a neuron in a higher-order area to neurons that are multiple synapses away?

Compared to what we know at the synaptic level, there is still very little clarity on what happens at a network level in order for learning to occur.

I. Physiology of neural networks

Nearly a century after the neuroanatomical organization of the cortex was first defined, its basic logic remains unknown. (Marcus, 2014)

It turns out that we actually don't know how things work on a network level. We have a couple hypotheses, and models for specific tasks and computations, but no "big-picture" understanding of the cortex's logic.

One hypothesis which has prevailed for 40 years is that the same canonical microcircuit is copy-pasted everywhere in the cortex (Creutszfeld, 1977). At the level of the cell, cortical slices appear plenty similar, featuring 6 distinct layers regardless of task and location.

Recently, Marcus et al. (2014) argue that actually, there is no canonical microcircuit, and that computational circuits vary widely from one area to the next. Pre-structured connectivity provides inductive biases in learning, so, for example, the sensory cortex would be rich in hierarchical circuits. Indeed, physiological evidence exists for differential organization between sensory areas (Scala et al. 2018) in the mouse.

The implication of the second hypothesis is that a certain amount of learning is "baked in" to the network—you would have separate circuit structures for object recognition and motor training, for example. Whereas in the first view, the brain starts off with just a cost function and limited structure, and acquires speciality through training and input data.

Connectomics

Connectomics, or the mapping out all of the neurons and synapses in the brain, would be able to answer large-scale questions about learning, namely about microcircuit uniformity or heterogeneity across areas. Although a full map of the mammalian brain seems far off, a joint effort by Janelia and Google has produced the world's first synapse-resolution map of a fly brain (2020), and in the process has developed segmentation techniques that may one day be relevant for mapping a mammalian connectome.

Whole-brain imaging of synapses requires resolution less than 20 nm for a system of millions if not billions of neurons (Xu et al. 2020). Clearly this is hard.

II. Constructing biologically plausible models

Simulations and mathematical models have long been used to investigate microcircuits and propose mechanisms for basic tasks. Recently, there's been a movement to create models with hierarchical structure, one of the hallmarks of deep learning. Hierarchical architectures are a strong inductive bias in learning and we have reason to believe they are prominent in brain neural networks. The task, then, is to reconcile hierarchical arrangements of neurons with the physiology of signal propagation.

The 'credit assignment' problem

Backpropagation, the learning rule used by deep ANNs, is unreasonable in the brain since it involves each neuron having knowledge of many thousands or millions of weights in other layers. Many models have been designed with biologically plausible learning signals, but they underperform compared to backpropagation. Scellier and Bengio (2016) introduced a model based on Hebbian rules, but it depends on symmetric feedforward and feedback weights.

The discovery here is that error signals can work in another way and still exhibit backpropagation-like performance. In this algorithm, the feedforward W is made to approach the feedback B^T throughout learning (the so-called "feedback alignment"). The feedback alignment algorithm achieves performance comparable to backpropagation in terms of learning rate and accuracy on linear problems and more complex non-linear problems like MNIST.

Simultaneous feedforward and feedback pathways

The problem with feedback alignment and similar proposals is that they assume the existence of a separate pathway for the error signal and neuron activation. There exists no physiological evidence for such pairings.

Guerguiev et al. (2017) argue for a novel model of neurons that compartmentalizes feedforward and feedback information. The model has priors from the mammalian cortex and implements integration of information in two separate parts of the same neuron: online computation in the somatic compartments, and weight updates in the apical dendrites. Using the same random weights approach as Lillicrap, Guerguiev presents a composable, multi-layer structure and achieves similar performance on MNIST.

Very recently, Payeur et al. (2020) proposed a burst-dependent model that performs as well as standard, gradient-based neural networks while relying on a lot of biologically reasonable mechanisms.

They design a learning rule where, given a presynaptic trace, a postsynaptic burst leads to LTP and a postsynaptic single spike leads to LTD.

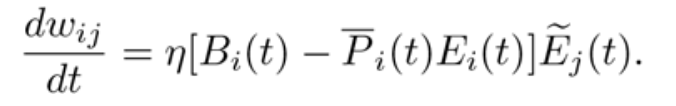
The equation describes the learning rule: namely, the change of the synaptic weight over time is a function of the learning rate, the burst train in the postsynaptic cell minus the event train, multiplied by the eligibility trace of the presynaptic cell.

Importantly, the rule reconciles the fact that feedback from higher-order areas cannot disrupt the online functioning of neurons—learning must be able to occur at the same time as sensory processing. Further, it allows for linearity in the feedback domain: information is conveyed in a graded fashion since the feedback signal is the probability an event is a burst.

The rate of an event (spike/burst) is the feedforward, normal processing of the neuron, while the probability that a given event is a burst is the feedback information from higher-order neurons. This clever manipulation is what allows for simultaneous processing of feedforward and feedback information, removing the constraint of symmetric weights in your network.

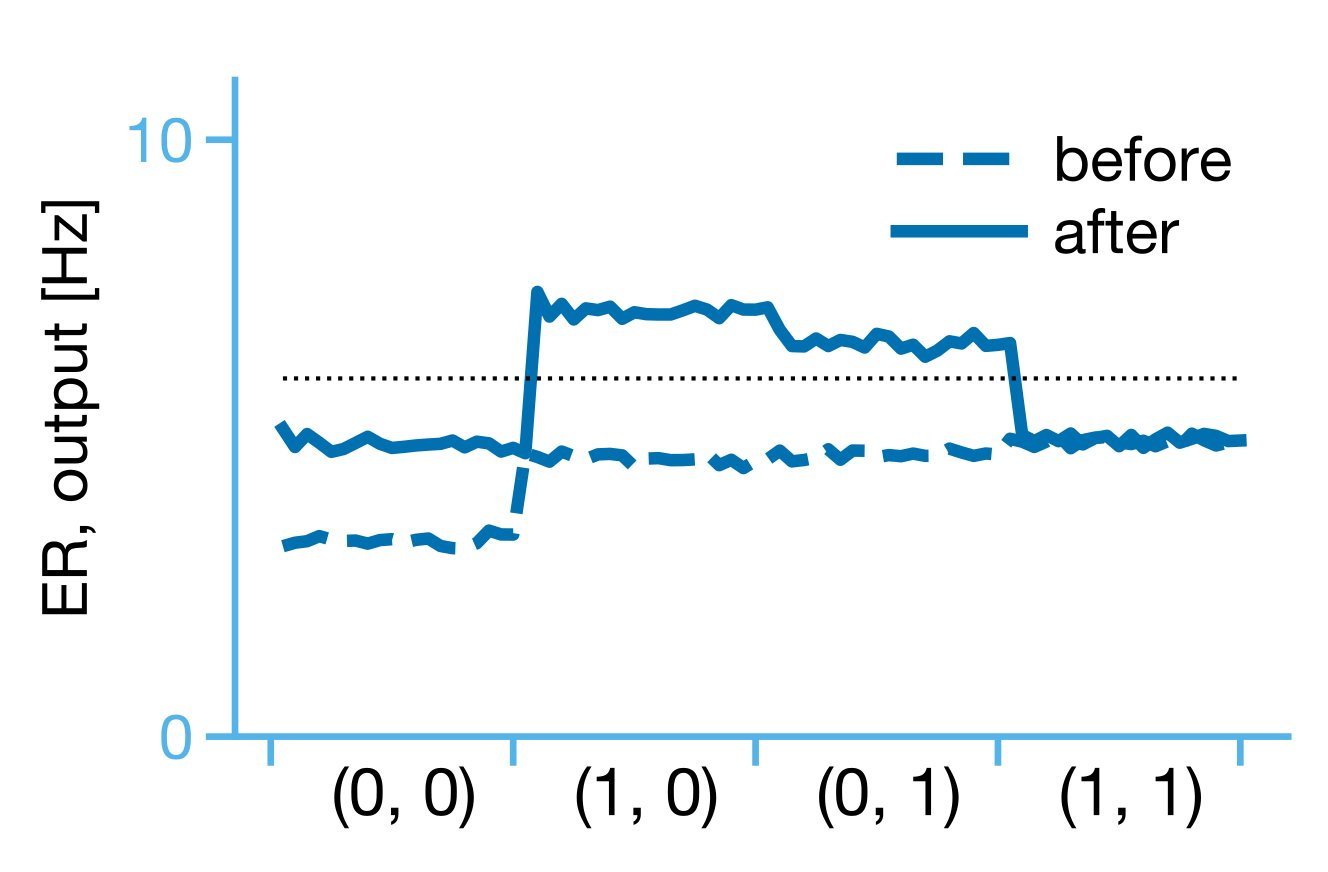
Importantly, once arranged in a hierarchy of 5 neurons (two input, one hidden, two output), the model was able to learn an XOR function of inputs. The proposed learning rule allows for multiplexing (simultaneous feedforward and feedback) and hierarchical credit assignment in an artificial neural network.

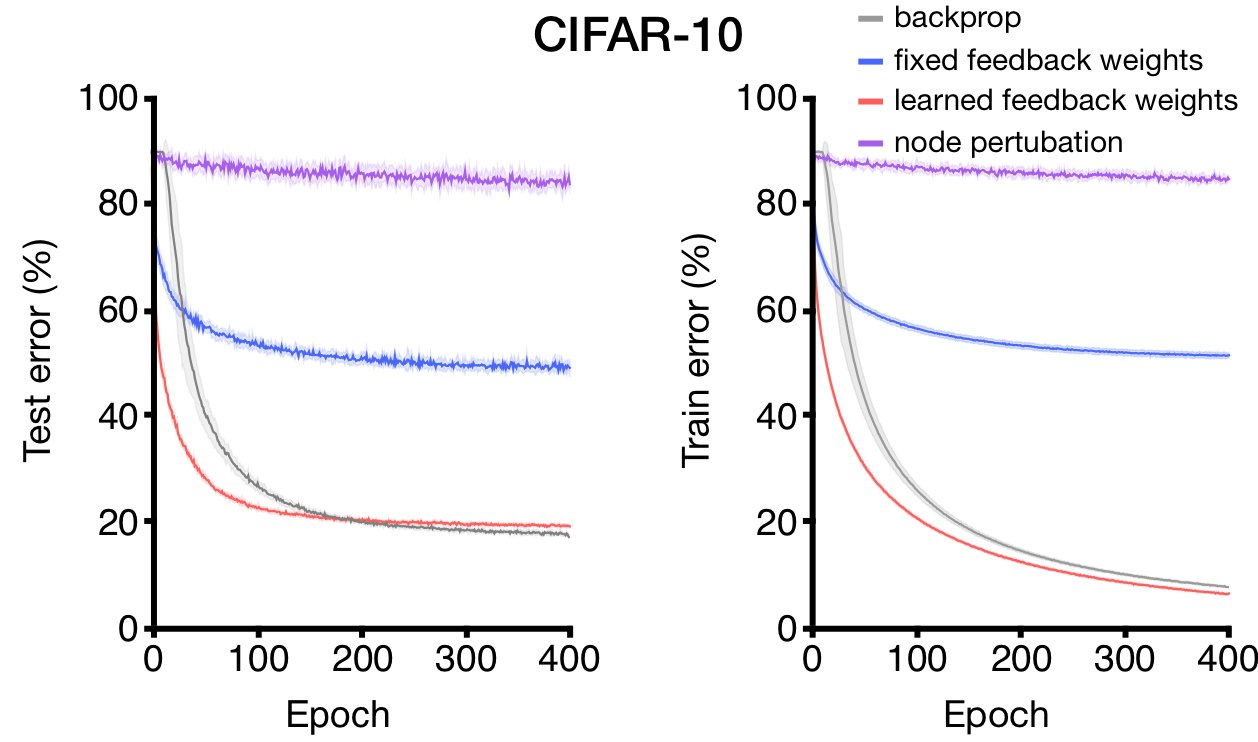
The authors extended their experiments by creating ensembles of burst-dependent neurons and training it on image data. The burst-dependent model significantly outperforms both feedback alignment (fixed feedback weights) and learning with a global reinforcement term (node perturbation).

Overall, biologically plausible learning models constitute a novel and promising approach to understanding human learning. However, it is worth noting that what you measure is what you make. A good number of these learning models are measured by their performance on linear tasks or simple classification tasks (MNIST), which makes sense because of their interpretability and limited computational requirements, but hazards the risk of guiding the models in very specific or undesired directions. Abstraction and transferability are key characteristics of human learning—tasks that better capture the complex environments we live in are desirable and ultimately necessary to form any notion of success in brain-based models.

III. Deriving insight from deep ANNs

In recent years, deep neural networks have achieved considerable success at tasks like image recognition. It's a tad remarkable that the design of a successful learning algorithm, one which is only shallowly modelled after the brain, has preceded the understanding of the actual learning algorithms in the brain.

ANNs are interesting because they show properties that classic von Neumann algorithms lack but are very much characteristic of human learning. As an example, CNNs show invariance to object position and lighting, and can generalize to unseen images.

As deep ANNs have continued to evolve, Schrimpf et al. (2018) set about to quantify how "brain-like" recent architectures are. Among other benchmarks, Schrimpf observes whether the artificial neurons are correlated with real recordings of ventral stream visual neurons of a primate. Artificial neurons are mapped to real neurons in the ventral stream with a linear transformation, and the predicted response on a held-out image is compared to the actual response to obtain a neural predictivity score.

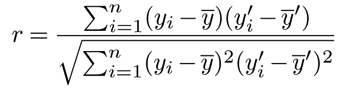
The Pearson correlation coefficient is computed between predicted and actual responses and aggregated across train-test splits.

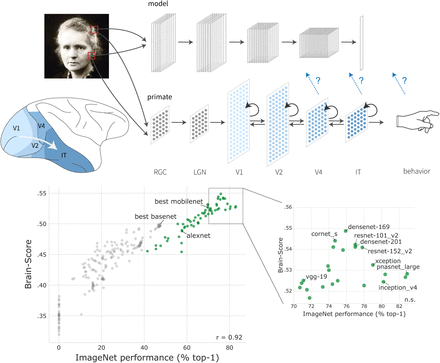
Figure 5 shows the results of their inquiry. Points in green are well-known, state of the art models, while points in grey are earlier ANN designs. ImageNet performance is plotted against the Brain-Score, an aggregation of benchmarks of neural similarity.

The brain-like-ness of ANN architectures is positively correlated with their performance—in other words, as ANNs have evolved to perform better at image recognition, they have also, without strictly trying, become more brain-like in their activations.

The interpretation of the paper is that internal representations of images are similar between artificial neural networks and the ventral visual cortical areas. We can infer that the architecture—the substrate—of learning in the brain is similar to the architecture of deep ANNs—that is, hierarchical, with ever-increasing receptive fields and assemblies of neurons that act as convolutional filters for certain features. Importantly, we learn that multiple layers of neurons are involved in learning a representation of an image, and that any plausible learning mechanism must involve modulation of neurons across multiple synapses.

We may not be able to conclude strictly that the mechanisms of learning in the brain mirror the mechanisms in ANNs, but as the evidence of structural similarity increases, the suggestion of functional similarity becomes a bit more reasonable.

It is worthwhile to recognize the type of data that is provided to the human. There are parallels with the world of machine learning:

If intelligence is a cake, the bulk of the cake is unsupervised learning, the icing on the cake is supervised learning, and the cherry on the cake is reinforcement learning (LeCun, 2016)

What LeCun refers to here is how data looks in the real world: the majority is not labelled, and rewards are scarce for the purpose of directing behaviour. And currently, the golden child of the field of AI is convolutional neural networks, an algorithm that relies on a surplus of labelled image data.

Similarly, in the human realm we are provided orders of magnitudes more unlabelled data than labelled data. As deep ANNs progress towards solving unsupervised or self-supervised learning tasks, we might find better parallels with human learning then.

How much do we know about learning?

At the end of the day, we don't have a complete story to tell, though it appears we've made a good start in three different directions. The future of learning more about learning will involve a combination of better tools to observe synaptic structures in the cortex, better metrics to assess biologically-inspired learning models, and emphasis on unsupervised learning in the domain of deep neural networks.

[1]. Bliss, T. V. & Lomo, T. Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. J. Physiol. (Lond.) 232, 331–356 (1973).

[2]. Creutzfeldt, O. D. Generality of the functional structure of the neocortex. Naturwissenschaften, 64(10), 507–517. doi:10.1007/BF00483547

[3]. D. O. Hebb. The Organization of Behavior. Wiley, New York, 1949.

[4]. J. Guerguiev, T. P. Lillicrap, and B. A. Richards. Towards deep learning with segregated dendrites. eLife, 6:e22901

[5]. Marcus, G., Marblestone, A., & Dean, T. (2014). The atoms of neural computation. Science, 346 (6209), 551–552. doi: 10.1126/science.126166

[6]. A. Payeur, J. Guerguiev, F. Zenke, B.A. Richards, and R. Naud. Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits. BioRxiv, 2020.

[7]. Scala, F., Kobak, D., Shan, S. et al. Layer 4 of mouse neocortex differs in cell types and circuit organization between sensory areas. Nat Commun 10, 4174 (2019). https://doi.org/10.1038/s41467-019-12058-z

[8]. B. Scellier and Y. Bengio. Towards a biologically plausible backprop. arXiv preprint arXiv:1602.05179

[9].M. Schrimpf, J. Kubilius, H. Hong, N.J. Majaj, R. Rajalingham, E.B. Issa, K. Kar, P. Bashivan, J. Prescott-Roy, K. Schmidt, et al. Brain-score: Which artificial neural network for object recognition is most brain-like? bioRxiv (2018), p. 407007

[10]. Xu, C.S., et al., A Connectome of the Adult Drosophila Central Brain. BioRxiv, 2020.