
RIJNDAEL
Advanced Encryption Standard
74.414 Assignment 3
November 15, 2000

1. Introduction to RIJNDAEL
Rijndael is the block cipher algorithm recently chosen by the National Institute of Science and Technology (NIST) as the Advanced Encryption Standard (AES). It supercedes the Data Encryption Standard (DES). NIST selected Rijndael as the standard symmetric key encryption algorithm to be used to encrypt sensitive (unclassified) American federal information. The choice was based on a careful and comprehensive analysis of the security and efficiency characteristics of Rijndael's algorithm.
Rijndael is an iterated block cipher. Therefore, the encryption or decryption of a block of data is accomplished by the iteration (a round) of a specific transformation (a round function). Section 3 provides the details of the Rijndael round function. Rijndael also defines a method to generate a series of subkeys from the original key. The generated subkeys are used as input with the round function.
Rijndael was developed by Belgian cryptographers Joan Daemen of Proton World International and Vincent Rijmen of Kathlieke Universiteit Leuven [2]. The algorithm that they developed was designed as an easily understandable mathematical structure that can be broken down into simple components. Daemen and Rijmen write in their proposal to AES that Rijndael was designed based on the following three criteria [6]:
Rijndael was evaluated based on its security, its cost and its algorithm and implementation characteristics. The primary focus of the analysis was on the cipher's security, but the choice of Rijndael was based on its simple algorithm and implementation characteristics. There were several candidate algorithms but Rijndael was selected because based on the analyses, it had the best combination of security, performance, efficiency, ease of implementation and flexibility.
2. Encryption Standards Selection
An encryption standard specifies a cyptographic algorithm that has been approved by a legitimate and respected institution. Such standards are public algorithms designed to protect sensitive information. The standards are often adopted by commercial applications. The Advanced Encryption Standard (AES) supercedes the Data Encryption Standard (DES) which was adopted in 1977, though forms of DES and Triple-DES will likely continue to be used.
The AES was chosen by computer scientists at the National Institute of Standards and Technology (NIST), which is an agency of the U.S. Commerce Department's Technology Administration. NIST works to strengthen the U.S. economy and improve the quality of life by working with industry to develop and apply technology, measurements, and standards [1]. The U.S. Secretary of Commerce Norman Y. Mineta is quoted saying that:
Once final, this standard will serve as a critical computer security tool supporting the rapid growth of electronic commerce...This is a very significant step toward creating a more secure digital economy. It will allow e-commerce and e-government to flourish safely, creating new opportunities for all Americans. [4]Obviously, the importance and application of the AES are apparent. Many cryptographic algorithms exist to address and attempt to solve the issue of information security. Many of these algorithms were candidates for the AES. NIST selected the AES based on its uncontested ability to provide good security. Though good security was the primary quality required of the winning formula, factors such as speed and versatility across a variety of computer platforms also were considered. In other words, the algorithms must be able to run securely and efficiently on large computers, desktop computers and even small devices such as smart cards [5].
The candidates' security was analyzed with respect to their ability to resist cryptanalysis, the soundness of algorithms' mathematical basis and the randomness of the output [10]. The characteristics of the algorithms were analyzed for flexibility, hardware and software suitability and simplicity. Cost was also important based on speed and the cost of hardware implementations.
3. Detailed Description of RIJNDAEL
Since Rijndael is an iterated block cipher, the encryption or decryption of a block of data is accomplished by the iteration (a round) of a specific transformation (a round function). As input, Rijndael accepts one-dimensional 8-bit byte arrays that create data blocks. The plaintext is input and then mapped onto state bytes. The cipher key is also a one-dimensional 8-bit byte array.
With an iterated block cipher, the different transformations operate in sequence on intermediate cipher results (states). The design of Rijndael is based on easily understandable mathematical concepts including finite field mathematics and linear algebra for matrix manipulation.
Key and Block Size
A prime feature of Rijndael is its ability to operate on varying sizes of keys and data blocks. It provides extra flexibility in that both the key size and the block size may be 128, 192, or 256 bits. Since Rijndael specifies three key sizes, this means that there are approximately 3.4 x 1038 possible 128-bit keys, 6.2 x 1057 possible 192-bit keys and 1.1 x 1077 possible 256-bit keys. To compare, DES keys are only 56 bits long, which means there are approximately 7.2 x 1016 possible DES keys. Therefore, there are on the order of 1021 times more AES 128-bit keys than DES 56-bit keys [5].
The Sub key and the Key Schedule The sub keys are derived from the cipher key using the Rijndael key schedule. The cipher key is expanded to create an expanded key and the sub key is created by deriving a 'round key' by round key. The required round key length is equal to the data block length multiplied by the number of rounds plus 1. Therefore, the round keys are taken from the expanded key.
To maintain a secure system, the expanded key is always derived from the cipher key. This method ensures that the expanded key is never directly specified, which would open Rijndael up to several cryptanalytic attacks against its key generation methods. Recall that the security of this system depends entirely on the secrecy of the key, as the design of the algorithm itself is public and contains no secrecy.
Whole Byte operations There are several mathematical preliminaries that define the addition and multiplication operations within a finite field and with matrices. When performing finite mathematics, the bytes are treated as polynomials rather than numbers, which can allow different and occasionally allows for more simple implementations.
Encyphering with Rijndael The Rijndael cipher is an interative block cipher. It therefore consists of a sequence of transformations to encipher or decipher the data. Rijndael encryption and decryption begin and end with a step to mix subkeys with the data block. This extra step is done as a protection against cryptanalysis. To encipher a block of data in Rijndael, you must first perform an Add Round Key step (XORing a subkey with the block) by itself, then the regular transformation rounds, and then a final round with the Mix Column step omitted. The cipher itself is defined by the following steps:
As shown in [10], the pseudo C code is:
Rijndael(State,CipherKey) {KeyExpansion(CipherKey,ExpandedKey);}
AddRoundKey(State,ExpandedKey);
For( i=1 ; iFinalRound(State,ExpandedKey + Nb*Nr);
And the round function is defined as:
Round(State,RoundKey) {ByteSub(State);}
ShiftRow(State);
MixColumn(State);
AddRoundKey(State,RoundKey);
The round transformation is broken into layers. These layers are the linear mixing layer, which provides high diffusion over multiple rounds. The non-linear layer which are basically applications of the Rijndael S-box. And the key addition layer which is simply an exclusive or of the round key and the intermediate state. Each layer is designed to have its own well-defined function which increases resistance to linear and differential cryptanalysis.
These layers are accomplished by four transformation steps. The Byte Sub step is a non-linear byte substitution. The Shift Row transformation is a cyclic shift. This is followed by the MixColumn step in which the columns of the State are considered as polynomials over a finite field and are modulo multiplied with a fixed polynomial. Finally, the Add Round Key step is performed.
The Byte Sub step is a non-linear byte substitution that operates on each of the 'state' bytes independently, where a state is an intermediate cipher result. The operation of this step is accomplished with a substitution table (S-box). ByteSub returns a word in which each byte from the incoming state are mapped by the S-box to corresponding bytes. The Rijndael S-box is simple, invertible and composed of two transformations. First, the multiplicative inverse of the data is taken in finite field space GF(28) and then an affine transformation is applied.
Diffusion is defined as the minimum number of active S-boxes in a linear or differential characteristic [10]. Diffusion is important because within block cipher cryptanalysis, almost all the attacks have a complexity that depends on the number of active S-boxes. The cryptanalytic complexity also is affected by the input/output correlation of the individual S-boxes.
Linear diffusion layer results in provable lower bounds on the number of active S-boxes. They have provable lower bounds for the nonlinear order, the difference to linear functions and the resistance to linear and differential cryptanalysis. [10]
The Shift Row step ensures that the different bytes of each row do not only interact with the corresponding byte in other rows. The rows of the State are cyclically shifted with different offsets. Row 0 is not shifted, Row 1 is shifted over C1 bytes, row 2 over C2 bytes and row 3 over C3 bytes. The shift offsets C1, C2 and C3 depend on the block length Nb [10].
The Mix Column step is where the different bytes interact with each other. It causes every byte in a column to affect every other byte. The state is viewed as polynomials and the transformation consists of matrix multiplication of the state with a multiplication polynomial over a fininte field. The mix column transformation step is the only place in Rijndael's round transformation that the columns are mixed. This step works with the Shift Row step to ensure that all parts of the block impinge on each other.
The Add Round Key step generates a new round key for the following round of transformations. The derivation of subkey material is defined in the section above entitled The Sub key and the Key Schedule.
The official Rijndael web site displays this image to promote understanding of the Rijndael round transformation [8].
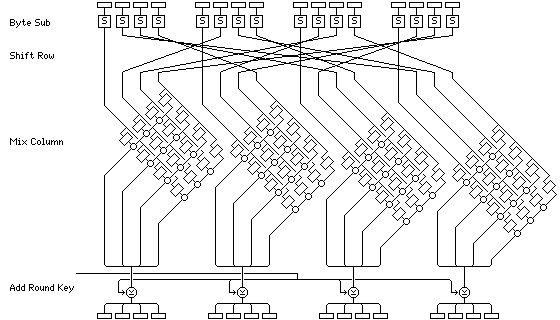
3.1 Strengths of RIJNDAEL
Daemen and Rijmen have specified Rijndael's advantages based on implementation aspects, simplicity of design, variable block length and extensions. Rijndael's implementation is very flexible since it can be used with varying key sizes and block sizes. It is also possible to change the sequence of some steps in Rijndael without affecting the cipher. The cipher is has a simple and elegant structure. It does not hide its structure by using complex components. Instead, it benefits from the advantages gained by the use of simple components in a well defined structure. Rijndael's security is based on the interaction of the cipher's individual components.
Rijndael is described as having a 'rich algebraic structure' which allows the cipher's security to be easily assessed in a limited time frame. This is an advantage over more complex designs that require extensive thinking, searching and 'bit tracing'. Rijndael is consistently a very good performer in both hardware and software across a wide range of computing environments. Its key setup time is excellent, and its key agility is good. Rijndael's very low memory requirements make it very well suited for restricted-space environments. There is additional security in that Rijndael's operations are among the easiest to defend against power and timing attacks.
The following scenario has been described to convey Rijndael's resistance to brute force attacks, "Assuming that one could build a machine that could recover a DES key in a second (i.e., try 255 keys per second), then it would take that machine approximately 149 thousand-billion (149 trillion) years to crack a 128-bit AES key. To put that into perspective, the universe is believed to be less than 20 billion years old. [5]" It also provides good security against linear cryptanalysis, differential cryptanalysis and opportunistic attacks.
3.2 Weaknesses of RIJNDAEL
Rijndael can be subject to standard techniques of differential and linear cryptanalysis. It is also weak to an attack called the "Square attack" that is based on the way matrix multiplication works, and because in GF(2^8), all the coefficients of the Mix Column matrix have reciprocals. However, in practical terms, this attack is not sufficient to compromise the security of the Rijndael algorithm.
Rijndael is also limited by its inverse cipher. Though the encryption is suited for many applications and is quite fast, the inverse cipher takes more code and cycles is not as well suited for different implementations, such as a smart card.
3.3 Comparison of RIJNDAEL to other AESs and DESs
Rijndael was chosen over four other candidate algorithms; MARS, RC6, Serpent and Twofish. Its performance was superior to all of the candidates for the large majority of performance analyses. Its encryption and decryption performance placed in the highest level for 64-bit (C and assembler), 8-bit (C and assmbler), 32-bit smartcard and for Digital Signal Processors. Its performance placed it in the second level when implemented with 32-bit C or Java. Its key scheduling performance placed in the first level for each platform. Therefore, AES concluded that Rijndael placed in the highest level for overall performance [10].
The Rijndael cipher algorithm was not chosen over the other AES candidates because it provided a higher level of security. NIST commented that each of the five finalists provided satisfactory and relatively equivalent security. So far, none of the ciphers have fallen to a cryptanalytic attack, though many have been attempted. Therefore, each cipher algorithm maintains a high level of security.
Rijndael was chosen because of the simplicity of its design. The design uses simple components with easily proven and verified properties. The simplicity of Rijndael's design and components provided an advantage over the other design candidates. Daemen and Rijmen write that "From the beginning, our design strategy was to use as simple as possible components, to define clear evaluation criteria, and to use simple components with easily provable properties where possible [9]". The other teams had some difficulty proving and analyzing their ciphers. Daemen and Rijmen state that [11] "both the Serpent design team and the MARS design team did not produce S-boxes that are in accordance with their own design criteria... and the key dependent S-boxes of Twofish have made it apparently very difficult to determine the security of the cipher.
4. Resources
1. http://csrc.nist.gov/encryption/aes/
2. http://www.ams.org/notices/
3. http://www.ams.org/notices/200003/200003-toc.html
4. http://www.nist.gov/public_affairs/releases/g00-176.htm
5. http://csrc.nist.gov/encryption/aes/round2/aesfact.html
6. Daemen, Joan; Rijmen, Vincent. AES Proposal: Rijndael.
Source: http://csrc.nist.gov/encryption/aes/rijndael/Rijndael.pdf
7. http://www.esat.kuleuven.ac.be/~rijmen/rijndael/sbox.pdf
8. http://home.ecn.ab.ca/~jsavard/crypto/co040801.htm
9. http://www.counterpane.com/rijndael.html
10. http://csrc.nist.gov/encryption/aes/round2/r2report.pdf