Dynamic Difficulty
When we think about difficulty in modern video games, we first think about choosing the difficulty from a menu: casual, normal and hardcore. From different discussion I had with game designers, they design the game with only one difficulty in mind. When it is time to make the game easier and/or harder, they arbitrary change in-game variables, for example the enemies' health, aim precision, bullet damage, etc. This foreseen difficulty is only optimal for one type of player. If you are not that optimal player, well the game is going to be too hard or easy for you, which will cause anxiety or boredom.
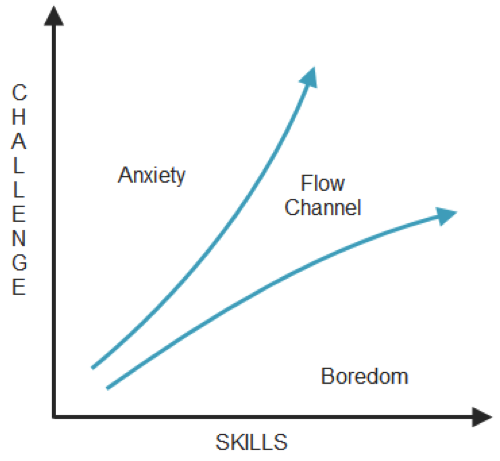
A different approach to building difficulty for the player is by letting different algorithm define values for in-game variables. For my master's thesis I used a ranking algorithm in order to determine the player's difficulty level. In greater detail, I used the ELO ranking system, after each combat the system was updated according to the outcome. In order to determine the difficulty of the combat, the rank is fed to the Artificial Intelligence and use to determine combat power, speed, reactivity, etc.
Before every combat you get to choose the spells you will use during combat, after that you will have to fight either the boss or the minion. When you win against the boss you will increase the level you are at. During combat, you have to answer the arithmetic questions correctly in order to fill the purple bar. When the bar is filled higher than one of the action bars, you can perform that specific action. You can click on the actions 1, 2 or 3, or use the keyboard Q, W or E key respectively. You can answer the questions using the keyboard as well.
The game is called Number to Number and uses adaptive difficulty. Moreover the system that determines the math questions uses adaptivity as well. The model is quite simple, it uses positive feedback model to increase/decrease the difficulty of the questions. For more information about the adaptive models used in this game, please feel free to consult my master's thesis in Publications.