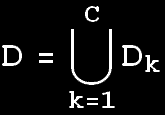Convex Hulls

The convex hull H(X) of a set of points X, is the smallest convex set that contains X. Informally, it is the smallest convex polygon that contains all of these points.

One can think of convex hull in 2D as a rubber band trying to enclose the points in. Therefore, it is called also the Convex Envelope. It can be shown also that for any set of points one convex hull exists.

Examples of convex hulls in 2D and 3D

A number of efficient algorithms to calculate the convex hull exist. A detailed treatment of convex hulls can be found in [4] and [5].

Statistical Geometry as a tool

In this project we are going to make use of geometry in classification.

That means also the objects and classes should be considered as geometrical structures.

Because each object is composed of a set of values (measurements), it can be considered a point in the space with its coordinates are the values of the object.

A class on the other hand is a collection of objects. Therefore, it can be considered as a set of points in the space.

Like other classification methods, we are going to make some assumptions about the objects (points) and the classes (sets). These assumptions will help us to reach a well defined result, and escape from the general case that is complicated, and in general no single model can describe it. However, the assumptions, should be consistent with the intuition, and should cover the more likely cases.

And from now on, we can use classes, sets and polygons interchangeably. Also points and objects.

We will assume that the classes are convex sets, or as a special case when the number of their elements is finite convex polygons or polyhedron in the general case.

The class k is denoted by Dk and the whole set of classes by D:

We will assume also that:

• The number of the points/objects in a set/polygon/class is indecent of the number of points in any other class. For instance, if many points lie in one class, which does not mean that, the other classes will contain a small number of points. It is simply not related and does not give a clue about the number of points in the other classes.
• The average number of points in a class (which is a convex polygon as we mentioned), is proportional to the area of the polygon. In other words, the larger, the more likely it contains more points. The opposite is true also.

 Theses two assumption imply also that the statistical model that describes the points is the “Stationary Poisson Process”, because it is the only process that realizes these conditions.

The stationary Poisson process has also several interesting properties:

1.      It is the most random one (maximal entropy).

2.      It is the limit (under rather general conditions) of sums of independent point processes (law of small numbers).

3.      Provided that n random points, generated by that process, are in the same region, they are independently and uniformly distributed in that region. So we can consider the most random repartitions.

To describe the size of a polygon in 2D we use the term area and in 3D we use volume (polygons become polyhedrons also). In higher dimensions; however, these terms don't apply. Mathematician introduced a general concept of measure that works on all dimensions called "Lebesgue measure".

You can think of Lebesgue measure (m) as a function that describes how big the polyhedron is. Area and volume are special cases of Lebesgue measure.

Finally, from now on, we will draw explanations in 2D. However, the discussion is general and valid for any number of dimensions.

Hani Safadi 2006 - I would be glad to hear your comments on hsafad @ cs dot mcgill dot ca