


Next: About this document ...
The Convex Hull of Random Hyperplanes
Let
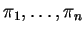 be hyperplanes in general position in
be hyperplanes in general position in 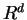 ,
,
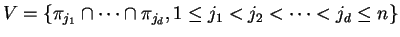 the set of vertices, and
the set of vertices, and 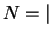 conv
conv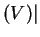 , the number of
extreme points of the convex hull of
, the number of
extreme points of the convex hull of 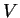 . We show that for
. We show that for 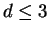 ,
if the
,
if the 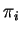 are chosen ``randomly'', there is a constant
are chosen ``randomly'', there is a constant 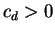 depending on
depending on 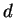 but not on
but not on 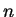 so that
so that 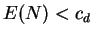 . The prospects for
. The prospects for
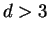 will be discussed.
will be discussed.
Adrian Vetta
2004-01-20