| maximize | 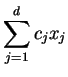 |
(12) | ||
| subject to | 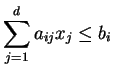 for all for all |
(13) | ||
A linear programming (abbreviated by LP) is to find a maximizer or minimizer of a linear function subject to linear inequality constraints. More precisely,
| maximize | 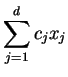 |
(12) | ||
| subject to | 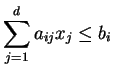 for all for all |
(13) | ||
| maximize | (14) | |||
| subject to | (15) | |||
Theoretically every rational
LP is solvable in polynomial time by both the ellipsoid method of Khachian
(see [Kha79,Sch86])
various interior point methods (see [Kar84,RTV97]).
The well-known simplex method of Dantzig (see [Dan63,Chv83])
has no known polynomial variants. In practice,
very large LPs can be solved efficiently
by both the simplex method and interior-point
methods.
For example, it is very easy on a standard unix station to solve an LP with
![]() and
and ![]() , while the vertex enumeration/convex hull
computation of the same size is simply intractable.
There are many commercial codes and public codes available.
See the LP FAQ [FG]. Two excellent books on LP are
Chvatal's textbook [Chv83] and Schrijver's
``researcher's bible'' [Sch86].
, while the vertex enumeration/convex hull
computation of the same size is simply intractable.
There are many commercial codes and public codes available.
See the LP FAQ [FG]. Two excellent books on LP are
Chvatal's textbook [Chv83] and Schrijver's
``researcher's bible'' [Sch86].