What is the best upper bound of the numbers of $k$-dimensional faces of a $d$-polytope with $n$ vertices?

Let $f_k(P)$ denote the number of $k$-faces of a $d$-polytope $P$, for $k=0,1,\ldots,d$.

The exact upper bound for $f_k$ in terms of $f_0$ and $d$. is known, thanks to McMullen's upper bound theorem.

The convex hull of distinct $n$ points on the moment curve $\{m(t)=(t^1, t^2, \ldots, t^d) : t\in R \}$ in $R^d$ is known as a cyclic polytope. It is known that its combinatorial structure (i.e. its face lattice, see Section 2.3) is uniquely determined by $n$ and $d$. Thus we often write $C(d, n)$ to denote any such cyclic $d$-polytope with $n$ vertices.

McMullen's Upper Bound Theorem shows that the maximum of $f_k(P)$ is attained by the cyclic polytopes.

Theorem 2 (Upper Bound Theorem)   For any $d$-polytope with $n$ vertices,

$$f_k(P) \le f_{k}(C(d,n)), \; \forall k=1, \ldots, d-1,$$

holds.

The number of $k$-faces of a cyclic polytope $C(d, n)$ can be explicitely given and thus one can evaluate the order of the upper bound in terms of $n$ and $d$.

Theorem 3   For $d \ge 2$ and $0 \le k \le d-1$,

$$f_{k}(C(d,n)) = \frac{n - \delta(n-k-2)}{n-k-1} \sum_{j=0}^{\lfloor d/2 \rfloor} \binom{n - 1-j}{k+1-j} \binom{n - k-1}{2j-k-1+\delta}$$

where $\delta=d-2 \lfloor d/2 \rfloor$. In particular,

$$f_{d-1}(C(d,n)) = \binom{n - \left\lfloor \frac{d+1}{2} \right\rfloor}{n-d} + \binom{n - \left\lfloor \frac{d+2}{2} \right\rfloor}{n-d}.$$ (1)

For example,

$$\begin{array}{lrrrrr} P & f_0 & f_1 & f_2 & f_3 & f_4 \\ C(... ...680 & 272\\ C(5,30) & 30 & 435 & 1460 & 1755 & 702 \end{array}$$

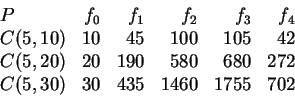
The upper bound theorem can be written in dual form which gives, for example, the maximum number of vertices in a $d$-polytope with $m$ facets.

Theorem 4 (Upper Bound Theorem in Dual Form)   For any $d$-polytope with $m$ facets,

$$f_k(P) \le f_{d-k-1}(C(d,m)), \; \forall k=0,1, \ldots, d-2,$$

holds.

The original proof of the Upper Bound Theorem is in [McM70,MS71]. There are different variations, see [Kal97,Mul94,Zie94].